在中学应该好好学但没人告诉你的几件事 – 第二部分：量词

---

量词 – 但实际上根本没有…

好吧，我不完全确定在每年的常规材料削减后，量词是否还存在于高中。也不太想检查，因为为什么要生气呢。

它们应该还在扩展课程中。真的应该。

好吧，但谁需要这个呢？

在大多数数学定义和定理中，使用的概念如：“每一个”和“存在”。

通常是在一些更复杂的序列中，例如“在每两个数之间有无数个数”（这有点半正式和不准确），或者：“每个非负实数存在且只有一个平方根”，或者：“存在某物，使得每个其他某物存在另一某物”（这是另一个东西的数学定义）。

在大学里，你会收到一大堆这样给出的定义和定理，快速在讲座中逐字逐句念出来，或者更糟的是，直接写在黑板上，形式如下：

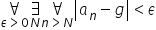
所以最好（而不是举手问教授是否应该“重新绘制”），你已经学会如何正确阅读这些公式。然后你可以直接进入“深入研究”定义的阶段，观察它在具体示例中的运作情况等等。

一般量词和特定量词 – 让我们更好地了解它们

“每个”，“对于每个” – 这是一般量词，表示为：。

“存在”，“存在这样的” – 这是特定量词，表示为：。

我使用并推荐这些量词符号，因为它们肯定不会混淆。

– 是倒写的字母A（来自英文“all” – 每个）。

– 是倒写的字母E（来自英文“exists” – 存在）。

也有其他表示量词的符号：Λ（“对于每个”）和V（“存在”） – 但我不会使用这些，因为它们容易混淆。

使用量词书写的数学公式

最简单的公式是：

– 我们读作：“对于每个x”（也可以写作：，但容易混淆，所以我不会这样做）

– 我们读作：“存在x”

然而，通常公式更复杂，例如：

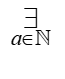– 我们读作：“存在一个是自然数的a”，或者：“存在一个a，属于自然数”，或者任何其他中文表达，反映事情的本质，即：

1. 存在a

2. a是自然数

这里没有关于每个单词必须是什么以及是否必须是“存在a”或“存在这样的a”的“硬性”语言规则。

公式可以并且通常需要彼此结合，例如：

\underset{x>4}{\mathop{\forall }}\,\underset{n\in\mathbb{N}}{\mathop{\exists }}\,

意思是：

“对于每个x>4，存在一个n属于自然数”

我们理解为，对于每个x>4，“找到”一个n属于自然数，以便对于每个这样的x“选择”合适的n。量词彼此逻辑相关，而不是彼此独立的公式。

更多…

顺序很重要

与最后一个相同的公式，只是改变了量词的顺序：

\underset{n\in \mathbb{N} }{\mathop{\exists }}\,\underset{x>4}{\mathop{\forall }}\,

…我们会读作：

“存在一个a是自然数，这样对于每个x大于4 …”

我们理解为，首先我们有一个n（我们知道它存在），只有对于这个特定的n，对于所有x>4，某事发生。

例子 – 插曲

经典的例子是这里的函数序列的点收敛和一致收敛的定义，它们之间的区别只是…量词的顺序（我对这些定义稍作简化）：

点收敛：

一致收敛：

在一致收敛的定义中，最初在点收敛中的量词排在最后。不进入细节，这改变了整个公式的意义。

在点收敛中，首先（我们从左读起）我们选择任意一个x，然后阅读公式，得出结论，对于最初设定的x，序列中函数值和“极限”函数值之间的距离趋于无穷小。

在一致收敛中，首先确定适当的函数值之间的距离趋于无穷小，然后得出结论，对于任意x，这样做。

书写定义，定理

了解如何阅读量词后，数学定义和定理的书写对我们来说是开放的。例如：

\underset{x\in\mathbb{R}}{\mathop{\forall }}\,{{x}^{2}}\ge 0

我们会读作：“对于每个实数x，x的平方大于或等于零”，或者更好地说：“每个x的平方是非负数” – 我绝对支持以更生动的语言阅读定义和定理。

上述句子是正确的。我们也没有任何问题写假句：

\underset{a>0}{\mathop{\exists }}\,\underset{x>a}{\mathop{\forall }}\,\frac{a}{x}>1

我们会读作：“存在一个正数a，对于每个大于a的x，a除以x大于1”，这当然是错误的（因为正数除以比它大的数永远不会大于1，没有这样的数）。

现在我们来看前一个帖子中的序列极限定义：

我们会这样读（添加一些解释）：

“对于任意大于零，我们找到一个序列项的编号，这样对于序列中每个编号大于的项，距离（绝对值是距离）这个项和极限小于”

我们也可以使用更人性化的语言：

“不论我们在开始时设置多小的距离，我们找到一个序列项的编号，这样这个序列的所有后续项都比设定的初始距离更接近极限”