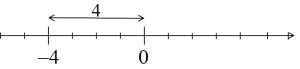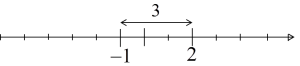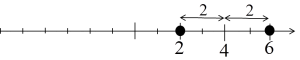如果你已经在大学里学习数学有一段时间了,你肯定会注意到高中学的多数内容在大学里不会直接派上用场。如果你刚刚开始学习数学,请注意这一点。
“直接”是什么意思?
我说“直接”是因为显然你在高中里为数学付出的每一滴汗水都不会白费,都会算在你的学习成果里。我的意思是抽象思维的训练、集中注意力解决问题的能力等等。
然而,直白地说,很多高中学习的数学内容你不再需要回顾,甚至都不用去看一眼。
不过,也有例外。
有些在高中学习的东西,如果没有掌握好,你在大学里就很难走远。
在学年的开始,值得重温或重新学习这些内容。这样你就为自己打开了通往新知识的大门。如果不学,这些内容会像鞋里的刺一样不断困扰你,阻碍(甚至是阻止)你前进的步伐。
这些并不是整个庞大的数学领域,而是一些小细节、小砖块,没有它们,整个建筑可能会倒塌。
极限的定义
以序列极限的定义为例,你会很快遇到它:
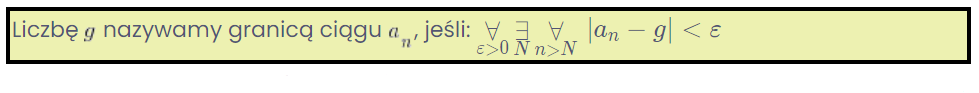
你理解左边这些奇怪的符号吗?还有右边的这个绝对值?不太多?
然而,要理解或至少正确读出这个定义,高中学的量词(左边这些怪物:![]() )和绝对值的几何解释(右边的)就应该够用了…
)和绝对值的几何解释(右边的)就应该够用了…
但是,我们不要抱怨,开始动手吧。在这篇文章和接下来的几篇文章中,我会向你展示一些细节,理解这些细节会极大地简化你的大学数学学习。
我们从…
1. 绝对值的几何解释(作为距离)
大概我们都知道绝对值是怎么回事。没有人会有问题,所以:
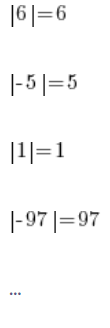
绝对值运算只是返回相同的数,如果是负数,则将其符号改为正。
它在几何上意味着什么呢?在数轴上?它就是从零开始的距离。例如,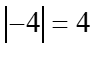 确实,数
确实,数![]() 到零的距离是4:
到零的距离是4:
我们会继续这个思路,并将绝对值理解为距离。
再注意一个事情:
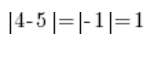
还有,在数轴上:
…就是说4和5之间的距离正好是4和5差的绝对值,无论我们减什么,因为:
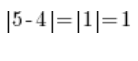
同样,如果我们减去3和8并计算结果的绝对值,我们得到的正好是数轴上3和8之间的距离(是5)。
这也适用于负数,例如-1和2:
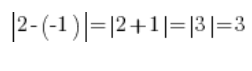
…就是说-1和2之间的距离:
你也可以自己玩玩。如果你有一本高中的课本,我强烈建议你花一个小时来研究这个话题,并进行一些练习。
我们可以总结出一个通用规则:
两个数之间差的绝对值:![]() 和
和 ![]() 等于它们之间的距离。
等于它们之间的距离。
例如,我们如何解读这样的方程:
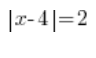
我们知道部分 ![]() 意味着未知数x与4的距离,而在等式的右边我们知道,这个距离应该 等于 2。
意味着未知数x与4的距离,而在等式的右边我们知道,这个距离应该 等于 2。
所以,方程的解将是与4的距离等于2的数,即2和6:
现在我们来看看这个不等式:
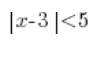
它的左边是x与3的距离,继续读下去我们得到信息,这个距离应该小于5。这一次,不等式的解将不仅仅是两个数,而是很多数 – 所有与3的距离小于5的数。在数轴上看起来像这样:
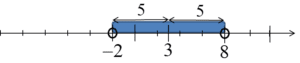
…就是说所有从-2到8的数,即数区间:![]() 。每个这样的数到3的距离小于5。
。每个这样的数到3的距离小于5。
这个数区间也可以称为点3的某个邻域(一个重要的术语,在大学里经常使用)。
用同样的方法推理,你可以找出满足不等式的数:![]() …
…
不过,这不是我的目标(你在高中时已经学过了,对吧 🙂 ?)。
然而,理解绝对值为距离是好的,因为它在你在大学里会遇到的很多数学定义中出现。因此,直接知道“这是怎么回事”是很好的。
例如,前面提到的序列极限:
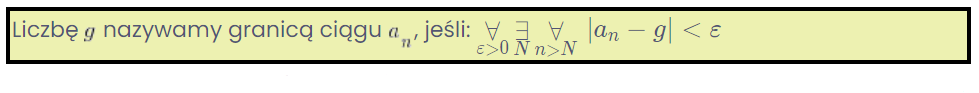
让我们现在集中在公式的右边。左边的符号留到下一个帖子中。
哪个解释更容易理解:
“![]() 和
和 ![]() 之差的绝对值必须小于
之差的绝对值必须小于 ![]() ”
”
还是:
“![]() 和
和 ![]() 之间的距离必须小于
之间的距离必须小于 ![]() ”
”
?
形式上,两种定义方式是等效的,但第二种方式更简单,更关注实质,不会被算术操作分散注意力。
理解绝对值为距离将极大地帮助你理解大学中看似复杂的许多数学定理和定义。
接下来呢?
在下一篇文章中,我将处理这些奇怪的符号:![]() 和
和 ![]() ,这样我们就可以完全理解我们的示例定义。
,这样我们就可以完全理解我们的示例定义。