数列的极限 – 讲座 1
主题：数列的极限——直观介绍与定义
摘要
在本文中，我将介绍什么是数列的极限，并进一步解释如何理解这一极限的定义。
什么是数列？
在我们讨论数列的极限之前，必须先说明什么是数列。数列是按照一定顺序排列的一组数字，例如：
1，2，4，7，10
上面是一个五项数列。顺序非常重要，例如：
2，1，4，7，10
这就是一个完全不同的数列。
当我们讨论数列的极限时，我们将处理 无穷数列，例如：
-4，-1，2，5，8，11，…
数列可以通过列出前几个项来表示，或者在可能的情况下，通过给出其一般项公式（例如第 100 项）。对于上面给出的最后一个数列（-4，-1，2，5，8，11，…），其一般项公式如下所示：
公式中的变量 n 表示数列中项的编号。让我们检查一下是否正确：
数列的第一项：
—— 正确（-4，-1，2，5，8，11，…）
数列的第二项：
—— 正确（-4，-1，2，5，8，11，…）
等等。
数列的例子。收敛数列。数列项在数轴上的表示。
为了理解什么是数列的极限，在数轴上用图形方式标出数列的各项会非常有帮助（请记住，从现在开始我们始终讨论的是无穷数列）。
例如，考虑数列 -4，-1，2，5，8，11，…（其一般项由公式 给出）。如果我们将它的前几项标在数轴上，结果如下所示：
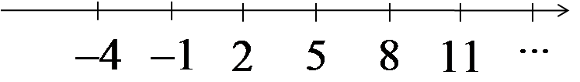
请注意，如果我们继续标出后续的项（14，17，…），这些点并不会接近数轴上的任何一个确定的数。恰恰相反，它们会越来越远地“逃向”无穷大。
现在来看另一个数列：
0，-2，-4，0，7，1，-2，2，2，…
为这个数列写出第 n 项的一般公式几乎是不可能的，因为它的各项产生得相当混乱，没有明显规律（尽管有人认为总是存在某种公式）。如果我们将这些项标在数轴上，会得到如下结果：
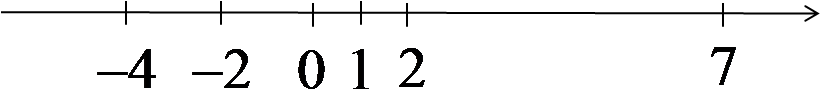
在标出连续的各项时，这些点会在数轴上来回跳动，并不会趋近于任何一个数。这样的数列也是存在的。
现在让我们来看下面这个数列：
可以观察到，分子是连续的自然数，而分母是比分子大 1 的数。这个数列的一般项是 
。将该数列的各项标在数轴上，我们会发现：
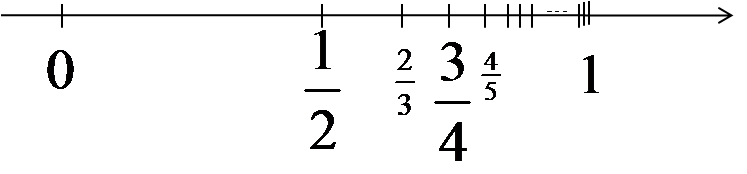
这个数列的各项越来越接近数字 1。例如，第 100 项（通过在公式 中代入 n = 100 计算）等于 
，非常接近 1。第 101 项更接近，第 102 项更接近。第 1000 项 
已经“几乎”等于 1。
随着项号越来越大，数列的各项会越来越接近 1。尽管数列中的任何一项都不等于 1（因为一个数除以比它大 1 的数永远不可能等于 1），但我们可以说这个数列的极限等于 1。
以上内容是对数列极限的一种非正式、直观的理解。我并没有精确定义“越来越大”和“越来越接近”究竟意味着什么。我们将在下一部分中对其进行严格定义。
在我们正式给出数列极限的定义之前，还必须回顾一个重要的概念：如何计算数轴上两点之间的距离。
数轴上两点之间距离的公式
考虑数轴上的两个数（为了说明问题，一个为正数，一个为负数）：
我们都知道它们之间的距离是 6，但如何快速计算呢？
一种方法是用较大的数减去较小的数。在本例中，用 2 减去 -4，结果为 
。这种方法是正确的，但在减法之前需要先比较大小，在处理变量时会比较麻烦。
因此，可以采用另一种方法：不管顺序如何，直接相减，然后取结果的绝对值。例如，用 -4 减去 2 得到 
，或者用 2 减去 -4 得到 
。
因此，数轴上两个数之间的距离等于它们差的绝对值。
数列极限的定义
现在我们回到数列极限的定义。
定义
称数 g 为数列的极限，如果满足：
\underset{\varepsilon >0}{\mathop{\forall }}\,\underset{N}{\mathop{\exists }}\,\underset{n>N}{\mathop{\forall }}\,\left| {{a}_{n}}-g \right|<\varepsilon [/latex] 该定义可以这样理解： “对于任意 ε > 0，都存在一个数 N，使得当 n > N 时，aₙ 与 g 之间的距离小于 ε。”
无论 ε 取多么小，总可以找到这样的 N。因此，该数列的极限等于 1。