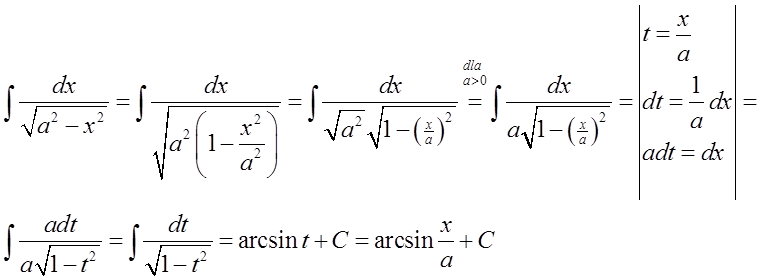被禁的未定积分公式 – 公式推导

---

大学教授有自己的要求。为了学生的利益，很多教授都会非常详细地规定解题规则。

我的不定积分课程的一位用户在GG上给我写了这样一段话：

我有个请求，您能在您的Facebook或博客上展示一下如何将您的积分公式变成纸上的形式吗？我指的是公式编号：5, 9, 10, 13, 14, 15, 16。很遗憾，我们的教授告诉我们只能使用最简单的公式，而我提到的那些更复杂的公式必须自己拆解成给定的形式。我想很多人会很感谢您的 🙂

指的是附在课程中的公式页：

不定积分公式

具体是指这些公式：

5.\quad \int{{{a}^{x}}dx=\frac{{{a}^{x}}}{\ln a}+C}

 

9.\quad \int{tgxdx=-\ln \left| \cos x \right|+C}

 

10.\quad \int{ctgxdx=\ln \left| \sin x \right|}+C

 

13.\quad \int{\frac{dx}{{{x}^{2}}+{{a}^{2}}}=\frac{1}{a}arctg\frac{x}{a}+C}

 

14.\quad \int{\frac{dx}{{{x}^{2}}-{{a}^{2}}}=\frac{1}{2a}\ln \left| \frac{x-a}{x+a} \right|+C}

 

15.\quad \int{\frac{dx}{\sqrt{{{a}^{2}}-{{x}^{2}}}}=\arcsin \frac{x}{a}+C}

 

16.\quad \int{\frac{dx}{\sqrt{{{x}^{2}}+q}}=\ln \left| x+\sqrt{{{x}^{2}}+q} \right|+C}

 

如果不是这些，那就是其他的

是的，教授们经常要求使用这些特定的公式，或者不使用某些公式。或者使用我们不喜欢的公式。

在这种情况下，唯一合理的办法当然是完全服从。在考试中，教授就是法律，没有必要事后抱怨教授没有通过考试，即使“应该”通过。

相反，我会逐一查看提到的公式，并展示如何应对每种情况（不幸的是，不能用一个共同的规则来涵盖它们）。“应对”意味着在不使用该公式的情况下，使用一个更具体的公式或通过代换来解决积分。

让我们逐一来看：

5.\quad \int{{{a}^{x}}dx=\frac{{{a}^{x}}}{\ln a}+C}

这个公式其实没什么好说的，它直接来自于求导公式的逆运算：

{{\left( {{a}^{x}} \right)}^{\prime }}={{a}^{x}}\ln a

所以在这里，我不会完全屈从教授的要求，而是请求解释如何计算 \int{{{3}^{x}}dx}而不使用公式 \int{{{a}^{x}}dx}。

如果有人有好的想法，拜托在帖子下的评论中分享给大家。

9.\quad \int{tgxdx=-\ln \left| \cos x \right|+C}

好了，回到正题。

这个公式不直接来自于任何求导公式的逆运算。

如果我们假设不认识这个公式，可以通过代换来计算积分 \int{tgxdx}：

10.\quad \int{ctgxdx=\ln \left| \sin x \right|}+C

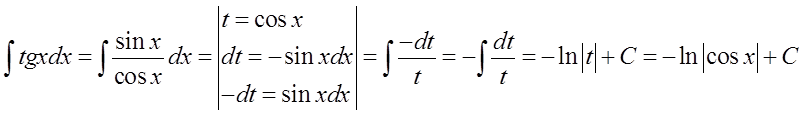
这里同样可以通过代换：

13.\quad \int{\frac{dx}{{{x}^{2}}+{{a}^{2}}}=\frac{1}{a}arctg\frac{x}{a}+C}

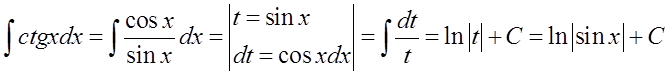
这个公式是以下公式的通用形式：

\int{\frac{dx}{{{x}^{2}}+1}=arctgx+C} 或者： \int{\frac{dx}{1+{{x}^{2}}}=arctgx+C}

教授的意思是要使用公式： \int{\frac{dx}{{{x}^{2}}+1}=arctgx+C}（这是由简单的求导逆运算得出的），而不是使用公式： \int{\frac{dx}{{{x}^{2}}+{{a}^{2}}}=\frac{1}{a}arctg\frac{x}{a}+C}（这是已经“处理”过的公式）。

我们通过转换和代换来实现这一点：

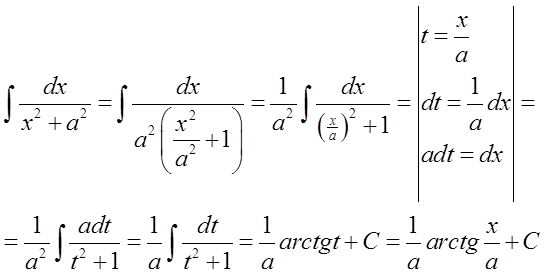
在具体例子中可能是这样的：

14.\quad \int{\frac{dx}{{{x}^{2}}-{{a}^{2}}}=\frac{1}{2a}\ln \left| \frac{x-a}{x+a} \right|+C}

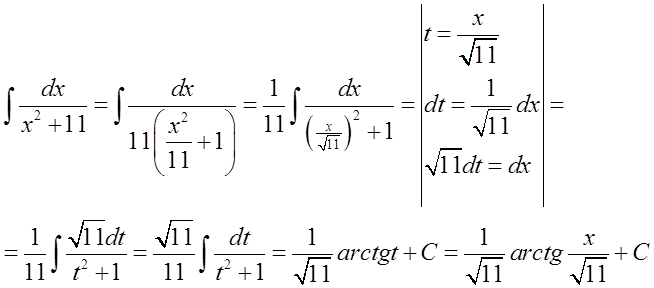
这个公式与前一个不同，不是要使用一个代换‘a’为‘1’的公式（没有这样的公式）。使用这个公式的替代方法是进行部分分式分解，就像在有理积分中那样（我在不定积分课程的第5课中展示了如何进行分解）。

实际上， \frac{1}{{{x}^{2}}-{{a}^{2}}}=\frac{1}{\left( x-a \right)\left( x+a \right)}然后可以进一步分解为部分分式。例如：

\frac{1}{{{x}^{2}}-9}=\frac{1}{\left( x-3 \right)\left( x+3 \right)} \frac{1}{\left( x-3 \right)\left( x+3 \right)}=\frac{A}{x-3}+\frac{B}{x+3}

然后乘以 \left( x-3 \right)\left( x+3 \right)，通过比较多项式来计算常数A，B，如我在课程第5课中展示的那样。

15.\quad \int{\frac{dx}{\sqrt{{{a}^{2}}-{{x}^{2}}}}=\arcsin \frac{x}{a}+C}

这里同样，通用公式： \int{\frac{dx}{\sqrt{{{a}^{2}}-{{x}^{2}}}}=\arcsin \frac{x}{a}+C}需要转化为特定公式： \int{\frac{dx}{\sqrt{1-{{x}^{2}}}}=\arcsin x+C}。

我们通过类似于公式13的方法来进行：

在具体例子中可能是这样的：

16.\quad \int{\frac{dx}{\sqrt{{{x}^{2}}+q}}=\ln \left| x+\sqrt{{{x}^{2}}+q} \right|+C}

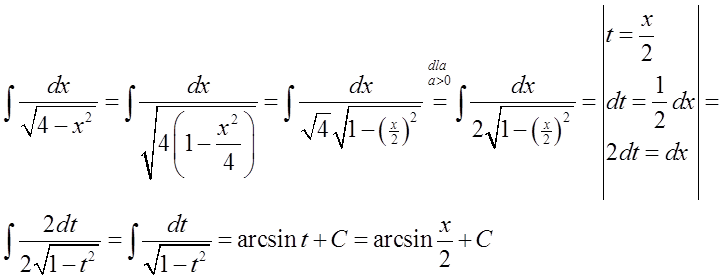
情况更加复杂，需要使用所谓的“双曲代换”（指双曲正弦和双曲余弦）。在这篇文章中我会暂时跳过这个话题，但很快我肯定会写关于这些代换的内容。

这些是用户问到的公式，我还要补充的是，我在基本公式列表中添加的公式：

\int{{{e}^{ax}}dx}=\frac{1}{a}{{e}^{ax}}+C \int{\sin axdx}=-\frac{1}{a}\cos ax+C \int{\cos axdx}=\frac{1}{a}\sin ax+C

可以通过简单的代换来推导： t=ax

例如，当我们有积分： \int{{{e}^{-x}}dx}并且由于教授的偏好不能使用公式 \int{{{e}^{ax}}dx}=\frac{1}{a}{{e}^{ax}}+C，我们使用代换 t=-x并继续计算。