No products in the cart.
Krystian Karczyński- 30 7 月 2024
- Komentarz 0
欧拉第一类替换（对于 a>0） – 复习
在之前的文章中：
我们讨论了以下类型的积分：
,
其中 a>0。
我们还解决了满足该条件的示例积分，即
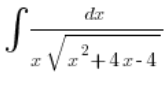
但是，如果在三项式中 
是负数 (可以忽略 a=0 的情况，因为那样就不会有二次三项式，积分可以通过更简单的替换解决 
，而不是欧拉替换)？
这时，我们可以（但不一定会）使用欧拉的第二类替换来帮助我们：
欧拉第二类替换（对于 c>0）
我们有以下类型的积分：
,
其中 c>0，我们使用以下类型的替换：
,
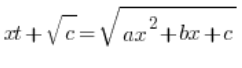再次将两边平方，此时带有 
的项消去，还需要将两边同时除以 
，以获得线性关系，从中我们可以通过变量 
依次求解：
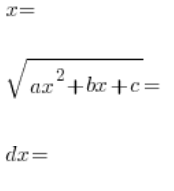
我们将这一切代入积分中：
我们再次得到有理积分，这种积分 – 我重复 – 通常是繁琐的。
让我们来看一个例子。
例子
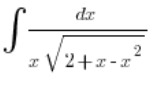
在二次三项式中成分的顺序有所变化，但显然 
。也就是说 不大于 
(因此我们不使用欧拉的第一类替换)，但 c>0（因此我们使用第二类替换）。
我们进行替换：
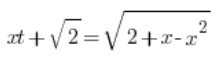
将两边平方：
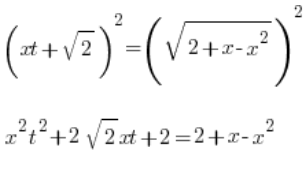
2 的项消去（就是这样的）：
现在我们将两边同时除以 x：
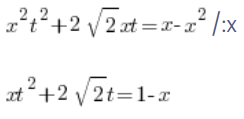
继续求解 x：
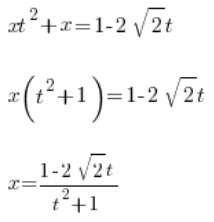
我们已经通过变量 t 求得 x。现在我们求解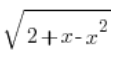 
。起初我们的替换是：
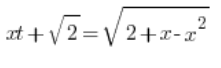
已经求出，因此只需代入：
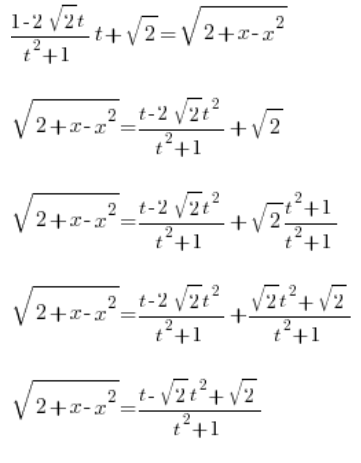
我们只剩下求 
。通过求 的导数来求解：
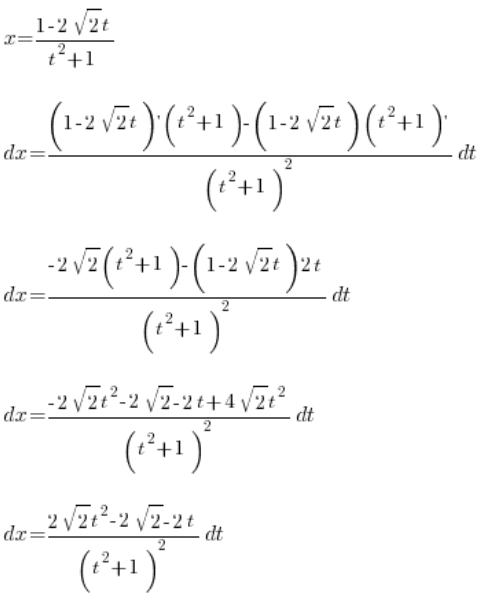
我们已经求得：
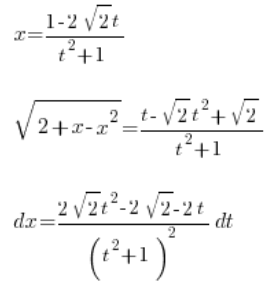
，全部通过变量 。我们进行积分：
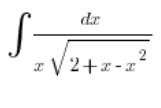
并代入：
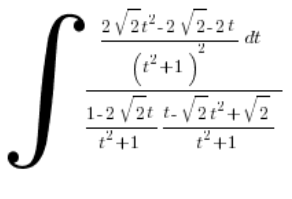
开始清理：
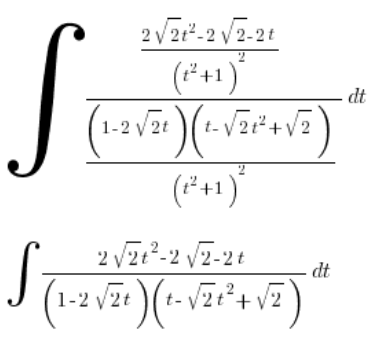
回到替换：
\frac{1}{\sqrt{2}}\ln \left| u \right|+C=\frac{1}{\sqrt{2}}\ln \left| 1-2\sqrt{2}t \right|+C还需要将 t 转换回 x。我们的欧拉替换是：
xt+\sqrt{2}=\sqrt{2+x-{{x}^{2}}}由此得出
t=\frac{\sqrt{2+x-{{x}^{2}}}-\sqrt{2}}{x}因此，我们的解为
\frac{1}{\sqrt{2}}\ln \left| u \right|+C=\frac{1}{\sqrt{2}}\ln \left| 1-2\sqrt{2}t \right|+C=\frac{1}{\sqrt{2}}\ln \left| 1-2\sqrt{2}\frac{\sqrt{2+x-{{x}^{2}}}-\sqrt{2}}{x} \right|+C其他情况呢？
我们知道，当积分中：
- a>0 – 使用第一类替换
- c>0 – 使用第二类替换
但是，如果既不是 ，也不是 大于零呢？在下一篇文章中我们将讨论欧拉的第三类替换，并展示该主题已经被覆盖，即对于每种类型的积分：
…我们将选择三种替换中的一种。
