让我们看看以下序列的极限:
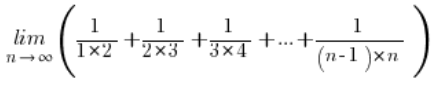
在这个问题中,我们感觉需要用序列求和公式 (算术或几何),但不幸的是,这个序列既不是算术的,也不是几何的…
怎么办?
我们需要用完全不同的方法。将每个分数分解成简单分数。这在处理不定积分有理函数时非常常见。关键是找到常数 A 和 B,使得…
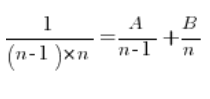
我们将上面方程的两边都乘以 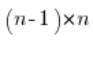 ,得到:
,得到:
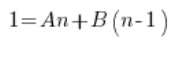
然后:
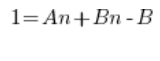
比较左边和右边的多项式系数 (多项式相等 – 高中知识) 我们得到了一个方程组:
![]() 从第二个方程中:
从第二个方程中: ![]() .
.
将其代入第一个方程:
![]()
我们也得到 ![]() .
.
因此我们可以将任意分数分解为:
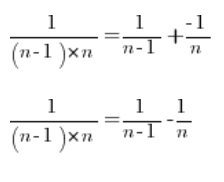
回到我们的序列极限,将每个分数分解为简单分数:
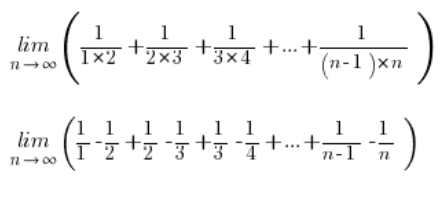
简化一些项后,我们得到:
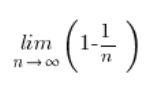
这个序列的极限显然不再那么可怕了:
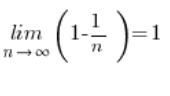
P.S.
你可以在我的视频课程中找到许多关于序列极限的有趣例子。


