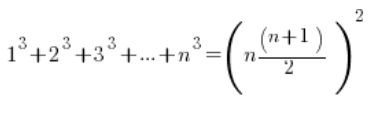Currently Empty: zł0.00
Krystian Karczyński- 5 8 月 2024
- Komentarz 0
在序列的极限中，有时是这样的：
有时甚至是这样的：
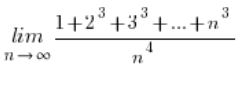
那怎么办？
答案很简单:
平方和和立方和的公式。
公式如下：
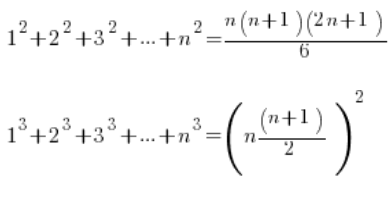
公式 – 就是公式 – 要记住。 如果你之前有类似的例子并且真的需要它们。
知道这些公式后，计算我们的极限变得非常简单：
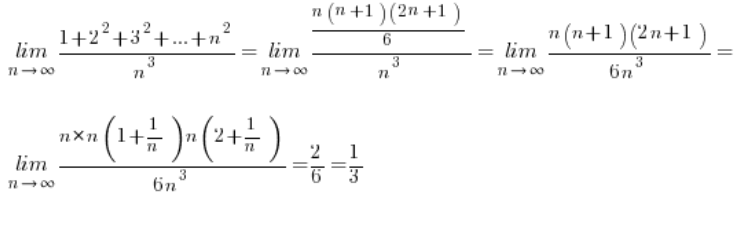
下一个极限：
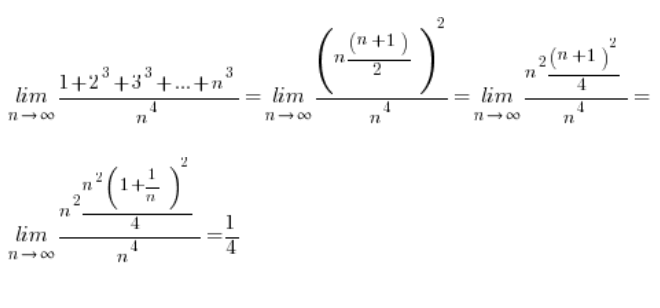
公式的归纳证明
公式的正确性可以通过归纳法来证明（至少在几年前这是高中标准）。 我将为以下公式做证明：
1. 
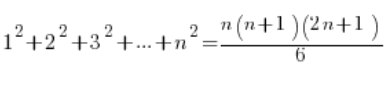
第一个归纳步骤
我们验证当 n=1 时公式的正确性：
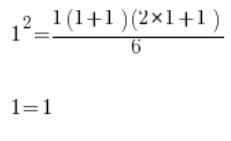
没错
第二个归纳步骤
我们假设 假设，对于某个自然数 n：
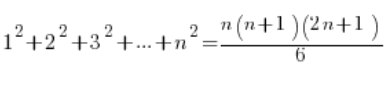
第三个归纳步骤
我们证明 结论（利用假设），对于 n+1 公式也成立，即：
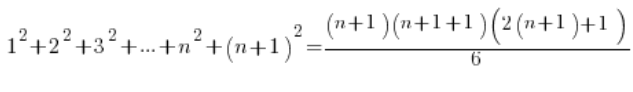
左边我们用假设中的公式代替 
，右边我们只是整理一下：
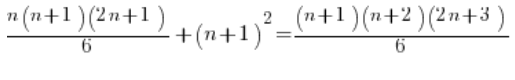
然后我们细致地操作，而不是粗暴地推导：
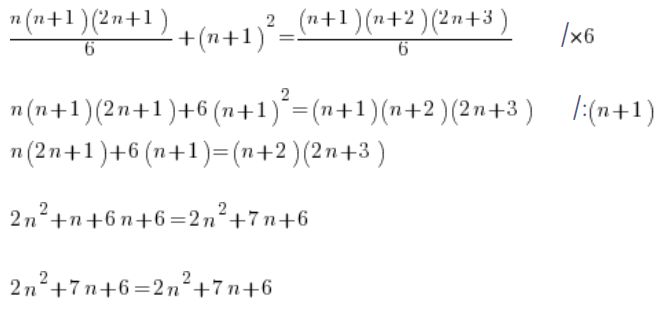
也就是说，结论得到了证明。 公式通过归纳法得到了证明。
我邀请你们用归纳法证明第二个公式，立方和：
