Currently Empty: zł0.00
Krystian Karczyński- 9 7 月 2024
- Comment 0
这篇文章是关于一个高考题的部分内容，这是一个高考学生通过邮件发给我的。不过出于好奇看看也无妨，而且以后再也别说大学数学比高中扩展数学难了。
🙂
题目部分
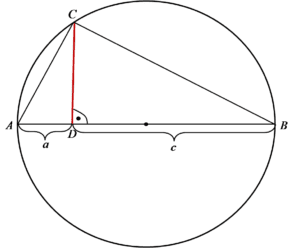
我们有以下情况：
需要证明标红的线段长度为 
。当然这只是整个题目的一小部分，猜猜它是什么？当然是关于数列的 🙂
所以在这里我们可以使用在直角三角形高度问题中常用的“三角形相似”这个所有高考学生的“最爱”。
1. 三角形 
（最小的那个）和
（最大的那个，内接于圆）是相似的（它们有两个相同的角：直角和<DAC，因此第三个角也是相同的，所以我们有AA相似）。三角形 
（中等大小的那个）和（再次最大的那个）也是相似的（它们有两个相同的角：直角和<CBD，因此第三个角也是相同的，所以我们再次有AA相似）。如果三角形 和 与 相似，那么它们也彼此相似，这就是我们要注意的：
相似于
2. 如果这些三角形是相似的，那么相应边的比例将相等。当然，我们选择包含标红线段的比例，我们将其长度表示为 
。
在三角形 中，最短边与中间边的比例为：
在三角形 中，最短边与中间边的比例为：
由于三角形是相似的，因此有如下等式：
3. 从这个等式中，我们求出 h，即标红线段的长度。我们像以前一样交叉相乘得到：
即：
这就是我们一开始要证明的。BINGO。
结论是：在直角三角形中求高（即落在斜边上的高当然），我们常常需要使用三角形相似，如上所述。
还有一个结论是，高中扩展数学确实可以很难。在大学里我们才能真正松一口气 🙂
