अनुक्रम की सीमा – व्याख्यान 1
विषय: अनुक्रम की सीमा – सहज परिचय और परिभाषा
सारांश
इस लेख में मैं यह समझाऊँगा कि अनुक्रम की सीमा वास्तव में क्या होती है। साथ ही, मैं यह भी स्पष्ट करूँगा कि इस सीमा की परिभाषा को कैसे समझना चाहिए।
अनुक्रम क्या है?
अनुक्रम की सीमा पर जाने से पहले, हमें यह समझना होगा कि अनुक्रम वास्तव में क्या होता है। संख्यात्मक अनुक्रम संख्याओं का एक क्रमबद्ध समूह होता है, उदाहरण के लिए:
1, 2, 4, 7, 10
ऊपर दिया गया एक पाँच पदों वाला अनुक्रम है। क्रम बहुत महत्वपूर्ण होता है। उदाहरण के लिए:
2, 1, 4, 7, 10
यह एक बिल्कुल अलग अनुक्रम है।
जब हम अनुक्रम की सीमा की बात करते हैं, तो हम अनंत अनुक्रमों पर काम करते हैं, उदाहरण के लिए:
-4, -1, 2, 5, 8, 11, …
अनुक्रमों को उनके पहले कुछ पद लिखकर प्रदर्शित किया जा सकता है, या यदि संभव हो, तो उनके किसी भी पद (जैसे सौवें पद) का सूत्र देकर। ऊपर दिए गए अंतिम अनुक्रम (-4, -1, 2, 5, 8, 11, …) के लिए ऐसा सूत्र इस प्रकार होगा:
![]()
सूत्र में चर n अनुक्रम के पद की संख्या को दर्शाता है। आइए जाँच करें कि यह सही है या नहीं:
अनुक्रम का पहला पद: ![]() – सही है (-4, -1, 2, 5, 8, 11, …)
– सही है (-4, -1, 2, 5, 8, 11, …)
अनुक्रम का दूसरा पद: ![]() – सही है (-4, -1, 2, 5, 8, 11, …)
– सही है (-4, -1, 2, 5, 8, 11, …)
आदि।
अनुक्रमों के उदाहरण। अभिसारी अनुक्रम। संख्या रेखा पर अनुक्रम के पद।
अनुक्रम की सीमा को समझने में संख्या रेखा पर अनुक्रम के पदों को ग्राफ़ के रूप में दर्शाना बहुत मददगार होता है (ध्यान रखें कि अब से हम हमेशा अनंत अनुक्रमों की बात कर रहे हैं)।
उदाहरण के लिए, अनुक्रम -4, -1, 2, 5, 8, 11, … लें (जिसका सामान्य पद सूत्र ![]() से दिया गया है)। यदि हम इसके पहले कुछ पदों को संख्या रेखा पर दर्शाएँ, तो यह कुछ इस प्रकार दिखेगा:
से दिया गया है)। यदि हम इसके पहले कुछ पदों को संख्या रेखा पर दर्शाएँ, तो यह कुछ इस प्रकार दिखेगा:
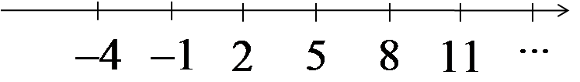
ध्यान दें कि यदि हम इसके अगले पदों (14, 17, …) को संख्या रेखा पर दर्शाएँ, तो वे किसी भी निश्चित संख्या के पास नहीं जाएँगे। इसके विपरीत, वे अनंत की ओर और अधिक “दूर भागते” जाएँगे।
अब एक और अनुक्रम देखें:
0, -2, -4, 0, 7, 1, -2, 2, 2, …
इस अनुक्रम के n-वें पद का सामान्य सूत्र निकालना लगभग असंभव है, क्योंकि इसके पद काफी अव्यवस्थित तरीके से बनते हैं और उनमें कोई स्पष्ट पैटर्न नहीं है (हालाँकि कुछ लोग मानते हैं कि हमेशा कोई न कोई सूत्र होता है)। यदि हम इन पदों को संख्या रेखा पर दर्शाएँ, तो हमें यह मिलेगा:
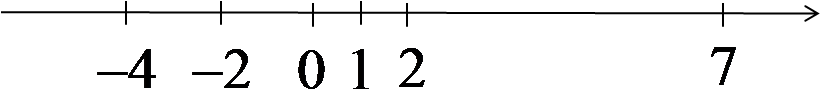
इन पदों को दर्शाने पर वे संख्या रेखा पर इधर-उधर कूदते रहेंगे और किसी भी संख्या के पास नहीं पहुँचेंगे। ऐसे अनुक्रम भी होते हैं।
अब निम्नलिखित अनुक्रम पर विचार करें:
![]()
देखा जा सकता है कि इसके अंश में क्रमागत प्राकृतिक संख्याएँ हैं और हर में उनसे 1 अधिक संख्याएँ हैं। इस अनुक्रम का सामान्य पद ![]() है। यदि हम इस अनुक्रम के पदों को संख्या रेखा पर दर्शाएँ, तो हम यह देखेंगे:
है। यदि हम इस अनुक्रम के पदों को संख्या रेखा पर दर्शाएँ, तो हम यह देखेंगे:
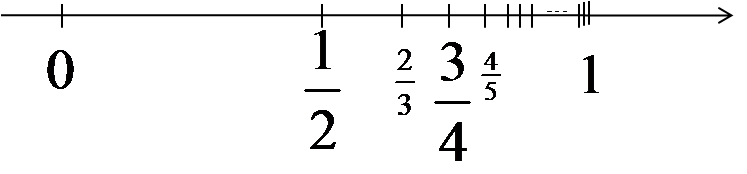
इस अनुक्रम के पद संख्या 1 के और अधिक निकट आते जाते हैं। उदाहरण के लिए, सौवाँ पद (जिसे सूत्र ![]() में n = 100 रखने पर निकाला जा सकता है)
में n = 100 रखने पर निकाला जा सकता है) ![]() के बराबर होता है, जो 1 के बहुत करीब है। 101वाँ पद और भी करीब होगा। 102वाँ उससे भी अधिक। हज़ारवाँ पद
के बराबर होता है, जो 1 के बहुत करीब है। 101वाँ पद और भी करीब होगा। 102वाँ उससे भी अधिक। हज़ारवाँ पद ![]() तो लगभग 1 के बराबर है।
तो लगभग 1 के बराबर है।
जैसे-जैसे हम पदों की संख्या बढ़ाते जाते हैं, हम 1 के और अधिक पास पहुँचते जाते हैं। यद्यपि अनुक्रम का कोई भी पद कभी ठीक-ठीक 1 के बराबर नहीं होता (क्योंकि किसी संख्या को उससे 1 अधिक संख्या से भाग देने पर परिणाम कभी 1 नहीं होता), फिर भी हम कह सकते हैं कि इस अनुक्रम की सीमा 1 है।
अब तक जो हमने देखा है, वह अनुक्रम की सीमा का एक अनौपचारिक, सहज समझ है। मैंने यह ठीक-ठीक परिभाषित नहीं किया कि “और बड़े” तथा “और पास” का क्या अर्थ है। हम इसे अगले भाग में सख्ती से परिभाषित करेंगे।
इससे पहले कि हम अनुक्रम की सीमा को औपचारिक रूप से परिभाषित करें, हमें एक बात अवश्य दोहरानी चाहिए: संख्या रेखा पर दो बिंदुओं के बीच दूरी कैसे निकाली जाती है।
संख्या रेखा पर दो बिंदुओं के बीच दूरी का सूत्र
संख्या रेखा पर दो संख्याएँ लें (एक धनात्मक और एक ऋणात्मक):
![]()
हम सभी जानते हैं कि इनके बीच की दूरी 6 है, लेकिन इसे सबसे जल्दी कैसे निकाला जाए?
एक तरीका यह है कि बड़ी संख्या में से छोटी संख्या घटा दी जाए। हमारे मामले में 2 में से -4 घटाने पर परिणाम ![]() मिलता है। यह सही है, लेकिन इसके लिए पहले संख्याओं की तुलना करनी पड़ती है, जो चरों के मामले में झंझट भरा हो सकता है।
मिलता है। यह सही है, लेकिन इसके लिए पहले संख्याओं की तुलना करनी पड़ती है, जो चरों के मामले में झंझट भरा हो सकता है।
इसलिए दूसरा तरीका यह है कि किसी भी क्रम में संख्याओं को घटाएँ और प्राप्त परिणाम का परिमाण (absolute value) ले लें। उदाहरण के लिए, -4 में से 2 घटाने पर ![]() मिलता है, या 2 में से -4 घटाने पर
मिलता है, या 2 में से -4 घटाने पर ![]() ।
।
अतः संख्या रेखा पर दो संख्याओं के बीच की दूरी उनके अंतर के परिमाण के बराबर होती है।
अनुक्रम की सीमा की परिभाषा
अब हम अनुक्रम की सीमा की परिभाषा पर लौटते हैं।
परिभाषा
संख्या g को अनुक्रम की सीमा कहा जाता है, यदि:
\left| {{a}_{n}}-g \right| < \varepsilon [/latex] इस परिभाषा को इस प्रकार पढ़ा जा सकता है: “प्रत्येक ε > 0 के लिए, कोई ऐसा N अस्तित्व में है कि प्रत्येक n > N के लिए, aₙ और g के बीच की दूरी ε से छोटी हो।”
अर्थात् ε चाहे कितना भी छोटा क्यों न लिया जाए, हम हमेशा ऐसा N खोज सकते हैं। इसलिए इस अनुक्रम की सीमा 1 है।
\underset{\varepsilon >0}{\mathop{\forall }}\,\underset{N}{\mathop{\exists }}\,\underset{n>N}{\mathop{\forall }}\,<
