Let’s calculate the rank of the matrix:
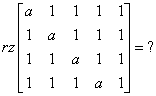
Solution
There are a few ways to approach this, and probably the quickest way is to multiply the fifth column by -1 and add it to the first, second, third, and fourth columns, resulting in:
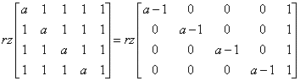Now, let’s take the determinant of the 4th-degree matrix:
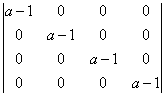A determinant where all elements except the main diagonal are zero is equal to the product of the elements on the main diagonal (I will prove this someday 🙂 ), so:
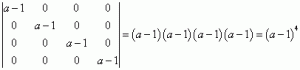This determinant is non-zero for all a not equal to 1. Therefore, for such a, the rank of our matrix, which we need to calculate, is 4 (because a non-zero 4th-degree minor can be extracted from it, and a larger one cannot).
What about the case where 
. We then get the rank of the matrix (substitute 1 for a):
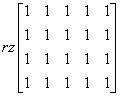And this rank is 1 (you can, for example, again use the fifth column on the others and eliminate the zero columns).
So, for a not equal to 1, the rank of the matrix is 4, and for a equal to 1, the rank of the matrix is 1.
