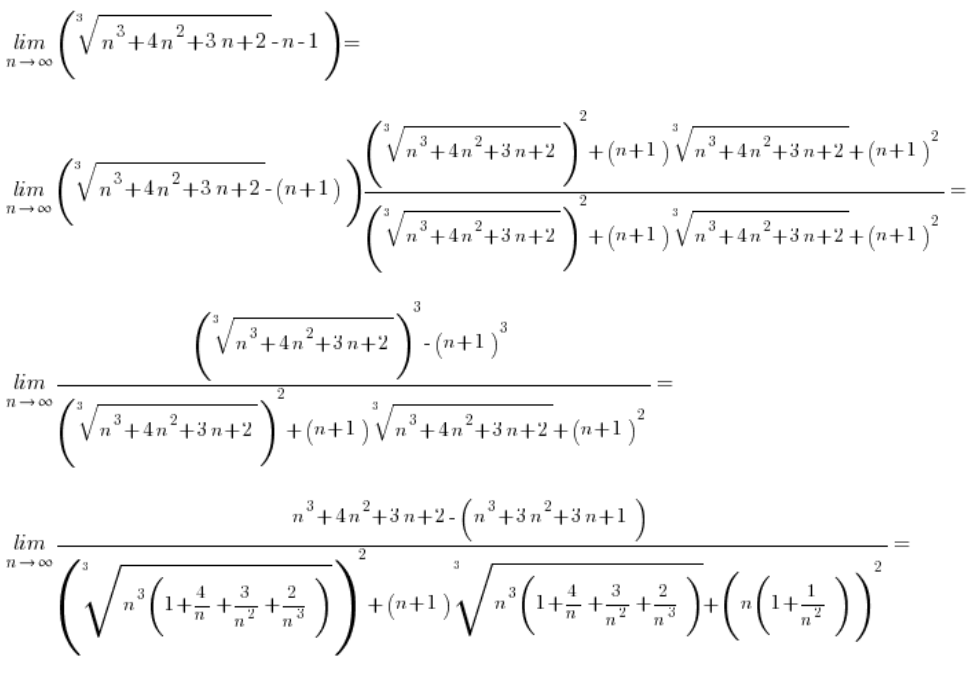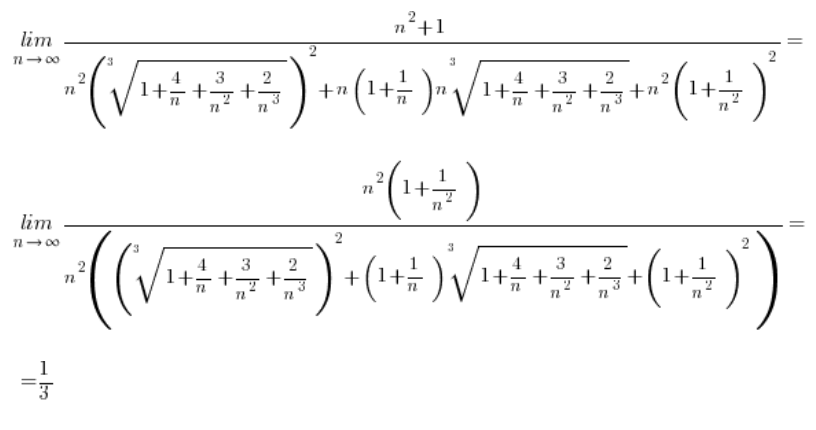Limits with Cube Roots (Is it Multiplication by Conjugate?)

---

How did it look with “normal” roots?

When we had to calculate a limit, which involved some subtraction with a root (and which couldn’t be calculated more simply, of course), like:

“Something – square root of something”

“square root of something – Something”

“square root of something – square root of something”

we used a trick I call – “multiplication by the conjugate.”

We simply multiplied this expression by its counterpart with a plus sign, or rather by a fraction where this counterpart was in the numerator and the denominator.

For example:

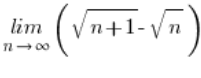 we multiplied like this: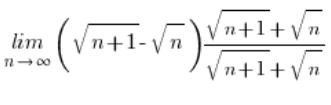

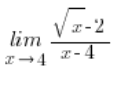we multiplied like this: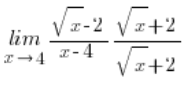

This clever trick allowed us to reach the pattern of the expanded multiplication formula:

Once we reached this pattern, the squares “canceled” the roots and we got to the simple result (well, sometimes a bit longer simple result).

But what about the situation when the roots involved in the subtraction are cube roots? Like here, for example:

\underset{x\to 8}{\mathop{\lim }}\,\frac{\sqrt[3]{x}-2}{x-8}

The standard method of proceeding, i.e., multiplying in the following way:

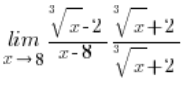
Won’t help us, because this time in the numerator, after reaching the pattern:

The squares won’t “cancel” the cube roots in any way. So, we’ll still be stuck.

How will it look with cube roots?

In the case of subtraction with cube roots, we simply need to “aim” for a completely different pattern (but also from middle school), namely:

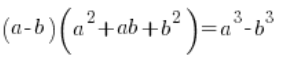
So, our given (where a or b or both are cube roots) instead of multiplying by we will multiply by and after applying the pattern, the cubes will do their job, “canceling” the roots.

Example 1

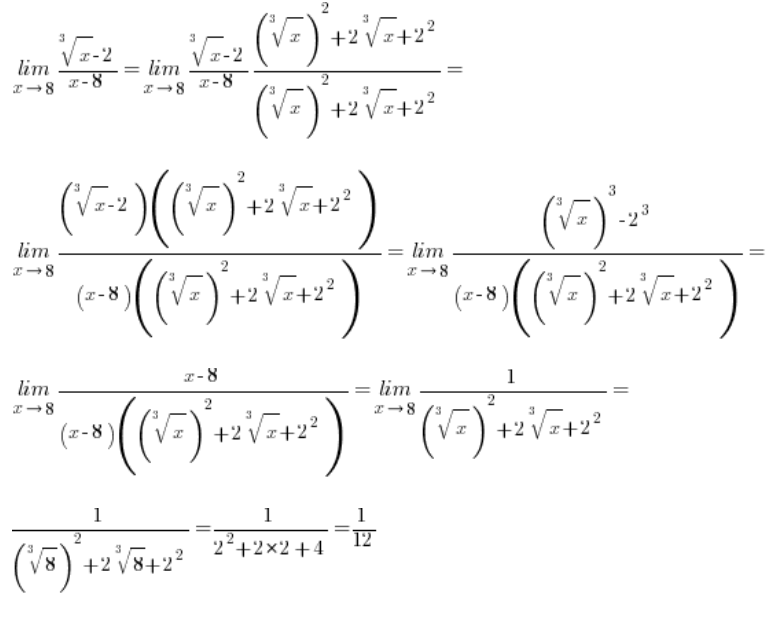
Example 2