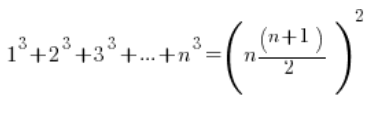In the limits of sequences, it sometimes looks like this:
and sometimes even like this:
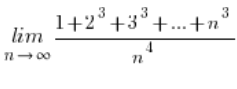
So what then?
The answer is simple:
formulas for the sum of squares and the sum of cubes of consecutive natural numbers.
They go like this:
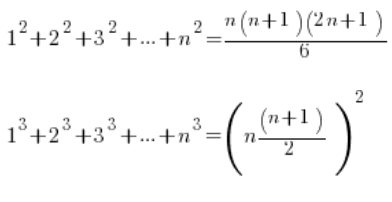
Formulas – just like any formulas – are to be memorized. If you’ve had similar examples and really need them.
Knowing these formulas, calculating our limits becomes trivial:
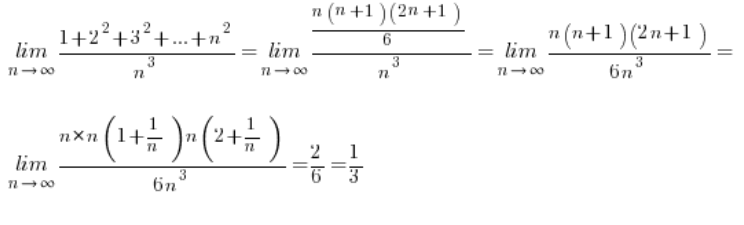
Next limit:
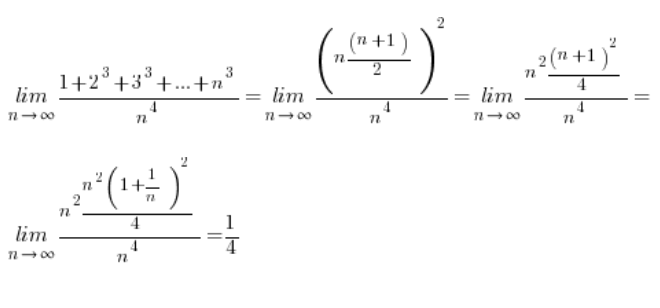
Inductive proofs for formulas
The validity of the formulas can be quite easily proven inductively (at least a few years ago this was a complete standard in high school). I will do this for the formula:
1. 
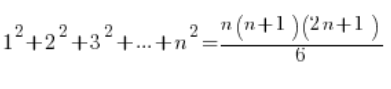
Step 1 of induction
We check the validity of the formula for n=1:
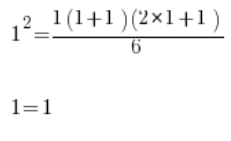
It matches
Step 2 of induction
We assume assumption, that for a certain natural n:
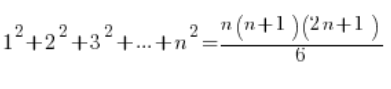
Step 3 of induction
We prove the thesis (using the accepted assumption), that for n+1 the formula also holds, i.e.:
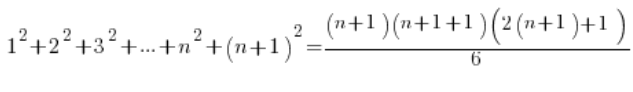
On the left side instead of 
we substitute the formula from the assumption, on the right we just organize:
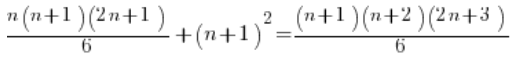
And then instead of forcing it, we work a little more subtly:
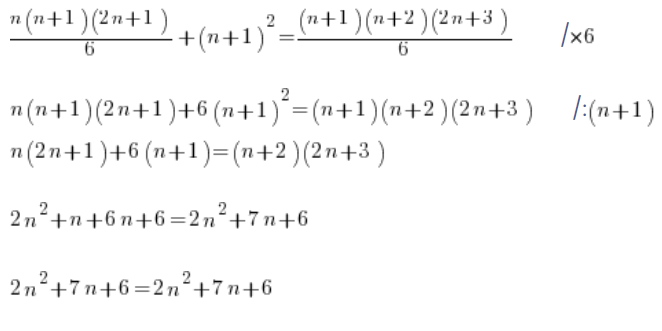
So the thesis is proven. The formula is proven inductively.
I invite you to inductively prove the second formula, for the sum of cubes:
