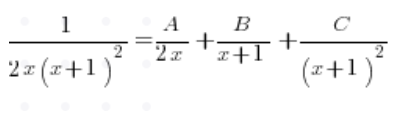Currently Empty: zł0.00
Krystian Karczyński- 29 April 2024
- Comment 0
Factoring a Quadratic Trinomial
In rational indefinite integrals, we often need to factor a quadratic trinomial: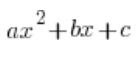 
. We do this of course using the formula: 
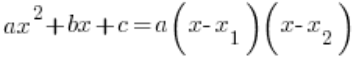, which works when 
.
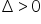Rational Integrals and Delta Equals 0
But how does this binomial look when Delta is precisely 0? For instance, how does this factor look: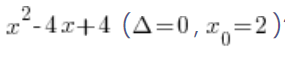 
?
Is it like this: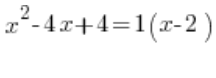 
?
Of course not… From high school, we remember that if 
then we get one root, but it’s a double root. So in our example, we can say: 
, meaning the quadratic trinomial factored looks like this:
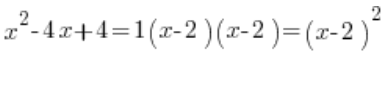
This has significant consequences for rational indefinite integrals when breaking them into simple fractions.
Example
Let’s take an example:
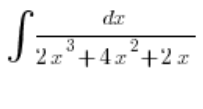
We break down the fraction by itself without the integral, writing:
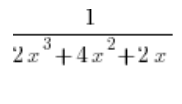
We factor out an x in the denominator:
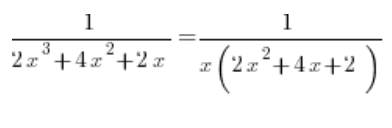
From the quadratic trinomial in the denominator, we compute the delta, which is 0, and get a root of (-1). Factoring it, we get:
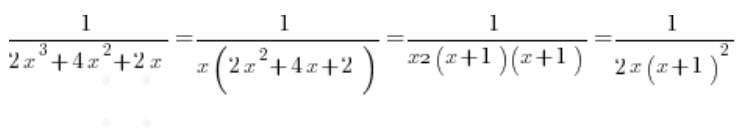
And breaking it down into simple fractions:
