Asymptotes Lecture 3
Topic: Oblique Asymptotes for Rational Functions
Summary
If we need to find asymptotes for rational functions — and only for them — we can compute oblique asymptotes (and thus also horizontal ones) completely without calculating limits, and sometimes just by looking at the function and writing down the answer right away. Since rational functions often appear in asymptote problems, learning a few additional “tricks” may be worth it.
First, let us recall what rational functions are. A rational function is a function made of two polynomials divided by each other, i.e.
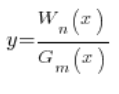– where 
and 
denote the degrees of the polynomials.
For example, these can be functions like:
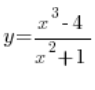(in the numerator we have a third-degree polynomial, and in the denominator a second-degree polynomial)
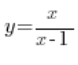(in the numerator and denominator we have first-degree polynomials)
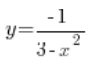(in the numerator we have a zero-degree polynomial, and in the denominator a second-degree polynomial)
How can we quickly find oblique asymptotes of such functions without calculating limits? The rules are simple. Everything depends on the degrees of the polynomials in the numerator and denominator. We have the following possibilities:
1) The degree of the numerator polynomial is at least 2 greater than the degree of the denominator polynomial
PROCEDURE: Oblique asymptotes do not exist. Write that as the answer. Done.
2) The degree of the numerator polynomial is exactly 1 greater than the degree of the denominator polynomial
PROCEDURE: An oblique asymptote exists. Divide the two polynomials (yes, the way it was done in high school), discard the remainder, and what you obtain is the equation of the oblique asymptote. Both as 
, and as 
. Write the answer. Done.
3) The degree of the numerator polynomial is the same as the degree of the denominator polynomial
PROCEDURE: A horizontal asymptote exists. Divide the leading coefficients (the coefficients at the highest powers) in the numerator and denominator, and the number you obtain is the equation of the horizontal asymptote. Both as , and as . Write the answer. Done.
4) The degree of the numerator polynomial is less than the degree of the denominator polynomial
PROCEDURE: A horizontal asymptote exists with equation 
. Both as , and as . There is nothing left to calculate. Write the answer. Done.
Examples
Problem 1
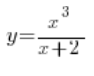
The degree of the numerator polynomial (3) is 2 greater than the degree of the denominator polynomial (1). There are no oblique asymptotes here.
Problem 2
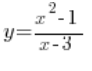
The degree of the numerator polynomial (2) is 1 greater than the degree of the denominator polynomial (1). We divide the polynomials (the way it was done in high school) and we get: 
with remainder 
. We write the answer that the line 
is the equation of the oblique asymptote as 
Problem 3
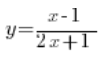
The degree of the numerator polynomial (1) is the same as the degree of the denominator polynomial (1). We divide the leading coefficients in the numerator and denominator and we get: 
. We write the answer that the line 
is the equation of the horizontal asymptote as
Problem 4
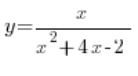
The degree of the numerator polynomial (1) is less than the degree of the denominator polynomial (2). We write the answer that the line is the equation of the horizontal asymptote as
The advantages of using such tricks are obvious (no need to struggle with limits), but the disadvantages are probably obvious too. First, it works only for rational functions (polynomial divided by polynomial). For other types, you have to use the standard methods. Second, you need to know how to divide polynomials at all — and in today’s hard times that skill seems to be slowly dying out (as of July 2010 it is still in the extended high-school math curriculum). Third, it is unclear how your professor will look at such “tricks”. On the other hand, I have seen professors who taught only this and did not bother students with ordinary limits at all.
So whether you will use it depends only on you. Good luck!
Click here to review oblique asymptotes (previous Lecture) <–
Click here to see selected functions that have asymptotes (next Lecture) –>