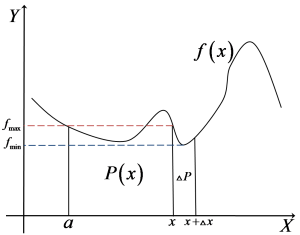Indefinite Integrals Lecture 2
Topic: Indefinite integrals and areas of regions.
Summary
In this lecture I will show a strange (so it would seem) thing. It will turn out that an antiderivative of the function 
can be interpreted geometrically as a certain area function associated with this function – something that seems completely unrelated to those velocities and sleds that I drew in the previous lecture.
What should you already know?
Before you start reading, you should already know what an indefinite integral and an antiderivative are (the previous Lecture).
Let’s begin. What function and what area are we talking about?
An indefinite integral is a family of antiderivatives of a certain function . Antiderivatives, i.e. functions whose derivative equals . Let’s draw our :
Is this function already our antiderivative? Of course not – an antiderivative is a function whose derivative gives the drawn .
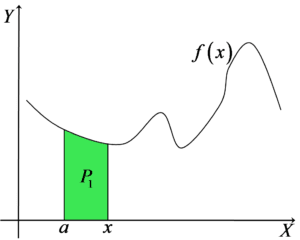
Let’s stir things up a bit in this drawing and mark the following area:
This is an area that may not be easy to compute (because it is not a basic geometric figure), but it certainly has some definite value, e.g. 10, or 
. For the moment, we are not concerned with what it is.
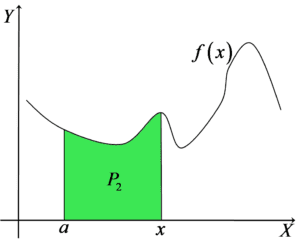
Assuming that 
is a constant and shifting 
we will obtain some other area:
And it is clear that by shifting this (we agree that is the boundary, i.e. 
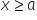) we will obtain different values of the area under the function :
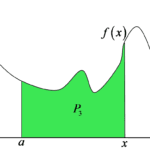
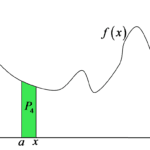
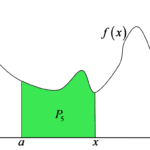
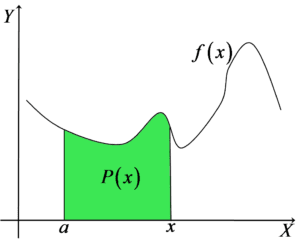
The area values will change depending on , so we can say that all areas constructed as above are values of some AREA FUNCTION depending on x. We denote it as:
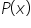
In general, on the drawing it can be marked like this:
We understand that for different arguments x we obtain different values of the area .
So we have two functions:
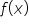
and
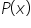
What is the relationship between them?
Ladies and Gentlemen, it is nothing less than this: one is an antiderivative of the other – or in other words, the second is the derivative of the first (from the previous Lecture we know that derivative and antiderivative are sort of “inverse” concepts).
We will show this next.
The area function P(x) is an antiderivative of f(x) – we prove it
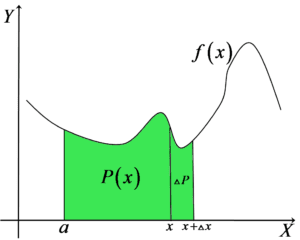
Let’s return to our graph and imagine that we shift x not by 1, nor by 10, nor by 
units to the right, but by some (for now) unspecified value 
:
After such an increment , our area will also increase by 
.
Now let’s mark the smallest and the largest value of the function on the interval 
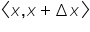as 
and 
:
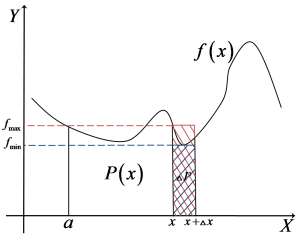
Each of them determines a rectangle (blue and red, respectively):
These are rectangles with one side equal to the segment of length and the other side equal to or . It is obvious (look at the figure and ask yourself whether it could be otherwise) that our area is greater than the area of the blue rectangle and smaller than the area of the red rectangle, i.e.:
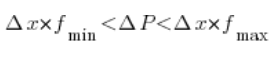
Dividing both sides of these inequalities by we obtain:
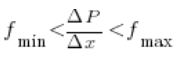
Now an important moment:
If our tends to 
, i.e. becomes infinitesimally small, then the values and will tend to , i.e. to the value of the function at the point x. Follow this on the last graph and imagine that the increment is smaller and smaller and smaller… How will and behave? They will get closer and closer to (in fact, in our particular drawing already now 
).
So if in the inequality:
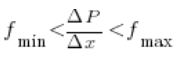
…for 
something happens such that:
and 
, it is obvious that 
(this is stated, for example, by the squeeze theorem).
So we have – writing the above symbolically:
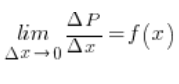
And what is the expression on the left-hand side of the equality? The ratio of the increment of the function value to the increment of the argument for an infinitesimal increment of the argument? As we remember from the lectures on derivatives, this is EXACTLY the derivative of this function.
So we have shown that:
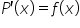
…that is, the derivative of the area function equals the function , or (which is the same) that:
THE AREA FUNCTION IS AN ANTIDERIVATIVE OF THE FUNCTION
Formula for the area
So we have the function and an antiderivative of it, the function . The indefinite integral was the family of all antiderivatives of the function. The function is therefore one of these functions. How does it differ from the others? From the previous Lecture we know that antiderivatives differ by a CONSTANT. Therefore, if we take as 
any other antiderivative of , we will get:
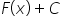
If in the equation above we take 
, we determine the constant C, i.e. the value by which differs from any other antiderivative:
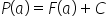
(look at our graph and see what happens when we take in it), that is:
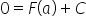
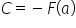
So, returning with the determined constant C to the formula we obtain:
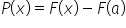
So we have a powerful formula for area. We can compute it… by integrating (finding an antiderivative and substituting appropriate values for and ). Powerful, because we are no longer limited to areas of circles, triangles, trapezoids (i.e. those for which we have “formulas”). We can calmly compute the area of irregular regions – lakes, forests, or whatever comes to mind.
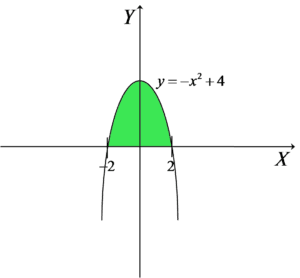
Example
Compute the area between the OX axis and the graph of the function 
.
On the graph, this area would look like this:
With this (after all very simple) problem, we would be completely helpless knowing only the high-school formulas for a trapezoid, parallelogram, circle, etc. Well, maybe not completely, because we could compute it “approximately” (for example by dividing the area under the parabola into small rectangles). But from today (or rather, since about the 17th century) we have additional artillery.
So we will use our formula for the area function:
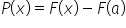
We take as our the “beginning” of the area on the OX axis, i.e. 
. We take as x the “end” of the area on the OX axis, i.e. 
. An antiderivative (found by integration) of the function 
is the function 
(a simple integral). So we have:
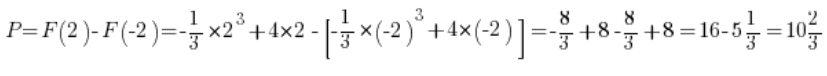
So the area under the parabola is exactly that. We can prepare the right amount of concrete to pour, or grass seed to plant, or whatever it is we needed 🙂
END
While writing this post, I used:
1. “Differential and Integral Calculus. Vol. II.” G.M. Fichtenholz. 1966 edition.
Click here to remind yourself what an indefinite integral is (previous Lecture) <–
Click here to return to the page with lectures on indefinite integrals