This post is dedicated to a piece of a high school exam question sent to me by a high school graduate via email. It’s worth taking a look out of curiosity and never repeating again that university math is harder than advanced high school math.
🙂
Piece of the Task
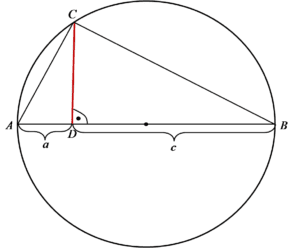
We have the following situation:
We need to show that the red segment has a length of 
. This is, of course, just a tiny part of the whole task. Can you guess what it’s about? Sequences, of course 🙂
So, we can use a frequently used trick in tasks involving the height of a right-angled triangle – similar triangles, which are everyone’s “favorite” in high school.
1. The triangles 
(the smallest one) and 
(the largest one, inscribed in the circle) are similar (they have 2 the same angles: right and <DAC, so the third angle is also the same, which means we have AA similarity). The triangles 
(the medium one) and (the largest again) are also similar (they have 2 the same angles: right and <CBD, so the third angle is also the same, so again we have AA similarity). If the triangles and are similar to , they are also similar to each other, and that’s what we notice:
is similar to
2. If these triangles are similar, then the ratios of the CORRESPONDING sides will be equal. Of course, we choose the ratios that contain the red segment, whose length we denote as 
.
In the triangle the ratio of the SHORTEST side to the MEDIUM side will be equal to:
In the triangle the ratio of the SHORTEST side to the MEDIUM side will be equal to:
Since the triangles are similar, there is an equality:
3. From this equality, we solve for h, the length of the red segment. We cross-multiply as we do in proportions and get:
Which means:
Which is exactly what we needed to show at the beginning. BINGO.
The moral is: when determining the height in a right-angled triangle (the one falling on the hypotenuse of course), we often need to use the similarity of triangles, as above.
And another is that advanced high school math could really bite. Only at university can we breathe easy 🙂
Ranti S
Is there a free trial before purchasing a course on eTrapez?
Telkom University Jakarta
Krystian Karczyński
No, unfortunately, there is no free trial.