Extrema of Functions – Lecture 5
Topic: Extrema of Functions
Summary
In this lecture, I will introduce the concept of extrema of functions intuitively and then define it in a precise way.
What Is an Extremum of a Function?
The word extremum comes from Latin and means the outermost or the extreme. There are two types of extrema of a function: minimum and maximum. Intuitively, this concept usually causes no problems:

Above we have the graph of the function ![]() , which attains a maximum at the point
, which attains a maximum at the point ![]() .
.
And we have no trouble with a minimum either, right?

Above we have a minimum of the function ![]() at the point
at the point ![]() .
.
If we think about it, there is no problem with a function having several extrema at different points:
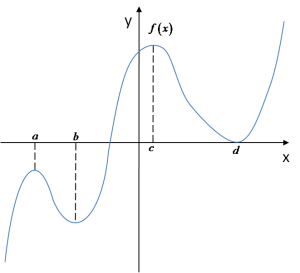
The function above has minima at points b and d, and maxima at points a and c. From this graph we can notice something important: Important note: Minima and maxima of a function must not be confused with the smallest or largest values of the function. These are completely different things.
Indeed, the value of the function at point d (a minimum) is greater than the value at point a (a maximum). So, speaking loosely but vividly, the “minimum” here is greater than the “maximum” (in terms of function values). Looking at the graph, how would you describe what an extremum is?
To introduce a precise and formal definition of an extremum, let us recall from previous lectures what a neighborhood of a point is:
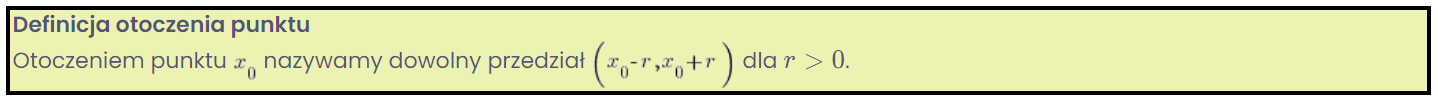
On our graph, I have marked two different possible neighborhoods of point b (I chose two different values of ![]() ). Of course, there are infinitely many of them:
). Of course, there are infinitely many of them:
Now that we know what a neighborhood is, we can define extrema of a function.

Let us look at the graph of our function and see how this definition “works” on it. We mark some arbitrary neighborhood of point b:
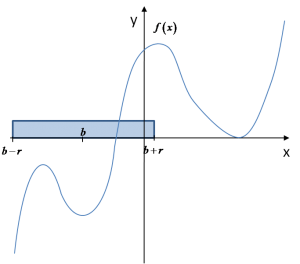
What values does the function take at points of this neighborhood? And what value at point b? Let us see:
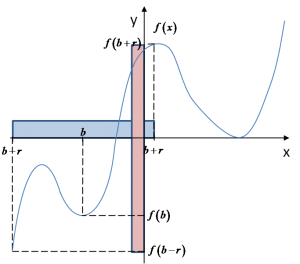
We can see that for this particular neighborhood of point b, the condition from the definition is NOT satisfied, that is:
– meaning that the value of the function at point is smaller than at any other point in this neighborhood (which would make it a maximum).
The condition tells us that the function value at the supposed extremum point (in our case, point b) should be smaller than the value at ANY other point in that interval. But from the graph we see that the value ![]() is not the smallest among the values in this neighborhood. So we certainly cannot speak about a maximum at point b in this neighborhood.
is not the smallest among the values in this neighborhood. So we certainly cannot speak about a maximum at point b in this neighborhood.
Does this mean that the function ![]() does not attain an extremum at point b? No!
does not attain an extremum at point b? No!
Let us carefully examine the definition. It states:
The function attains a maximum (or minimum) at point if there exists a neighborhood of point (contained in the domain of the function) such that for all other points in this neighborhood: … etc.
The key word in the definition is “exists.” It means that it is enough to find any neighborhood of point b that satisfies the condition. And that will not be difficult. Let us take, for example, the following neighborhood:
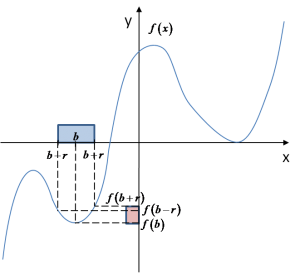
We see that for this neighborhood of point b, the function value at point b is indeed smaller than any other function value in that neighborhood. Therefore, the condition from the definition is satisfied, and we can say that the function attains a minimum at point b. There exists a neighborhood that satisfies the definition.
Very elegantly and somewhat old-fashioned, one might say: “there exists a neighborhood that fulfills the definition.” Try that phrase on your professors — maybe they’ll be so impressed that they’ll pass you for the semester without an exam 🙂
Notice that if we define extrema in this way (using neighborhoods), a function can attain an extremum at point ![]() only if it is defined on both sides of that point.
only if it is defined on both sides of that point.
For example:

This function ![]() does not attain an extremum at point
does not attain an extremum at point ![]() (even though it attains its smallest value there). There is no neighborhood satisfying the definition, because whatever neighborhood we take, to the left of
(even though it attains its smallest value there). There is no neighborhood satisfying the definition, because whatever neighborhood we take, to the left of ![]() the function does not take any values that could be compared with the value at that point. We cannot choose a neighborhood of
the function does not take any values that could be compared with the value at that point. We cannot choose a neighborhood of ![]() that lies entirely within the domain.
that lies entirely within the domain.
Note: To distinguish extrema from the largest and smallest values of a function, the following terminology is often used: extrema defined via neighborhoods are called local extrema, while the smallest and largest values are called global extrema. Of course, terminology is a matter of convention. Use what you prefer.
Good luck with extrema in your university battles! 🙂
THE END
While writing this post, I used:
1. “Differential and Integral Calculus. Vol. I.” G.M. Fichtenholz. 1966 edition.
Click here to review several asymptotes of well-known functions (previous Lecture) <–
Click here to see how extrema are related to derivatives (next Lecture) –>
Click to return to the page with lectures on analyzing functions
