Definite Integrals – Definition

Definite Integrals Lecture 1

Topic: Definite Integrals – definition

Summary

In the first part of the lecture I will show what a definite integral (in the sense of Riemann) is and how the corresponding series arises. In the second part I will introduce the strict, mathematical definition.

Part I – the definite integral as a certain series (sum)

As is often the case in mathematics, definite integrals did not just appear out of nowhere. Definite integrals solve a certain – completely simple to understand – problem. So first there was a PROBLEM, and only later did definite integrals appear. What was the problem?

The problem of calculating an exact area

Let us consider the issue of calculating the area of some region. We know the formulas for areas: circle, square, rectangle, parallelogram, trapezoid, rhombus, etc. That is nice.

But what if the region (e.g. a piece of forest) whose size we want to calculate is not such a regular: circle, square, rectangle, parallelogram, trapezoid, rhombus, etc.? Then we have a problem.

A way to calculate the area of an “irregular” region

In another lecture (devoted to indefinite integrals) I already presented one way to tackle this issue:

Indefinite integral and area calculation

In this lecture, however, we will try a different approach.

Let us draw an “irregular” region and introduce a coordinate system:

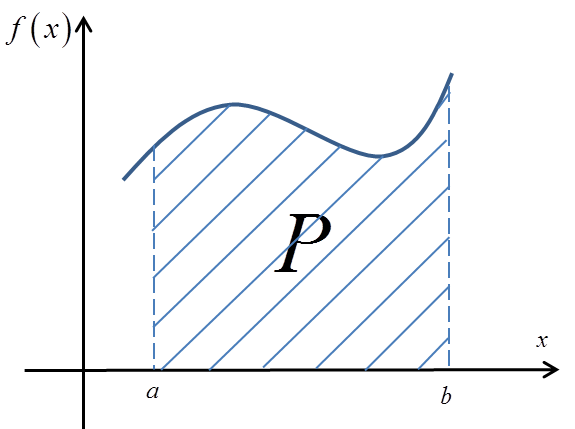
The region I have drawn can be called a “curvilinear trapezoid” (because one of its bases is a curve). If you think about it, practically any “blob” or irregular region can be divided into curvilinear trapezoids.

We assume that the function is already known, meaning that it is GIVEN.

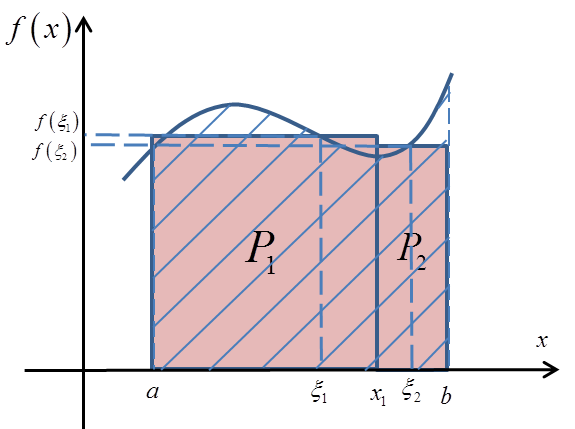
If so, we can quite easily calculate the areas of these two rectangles:

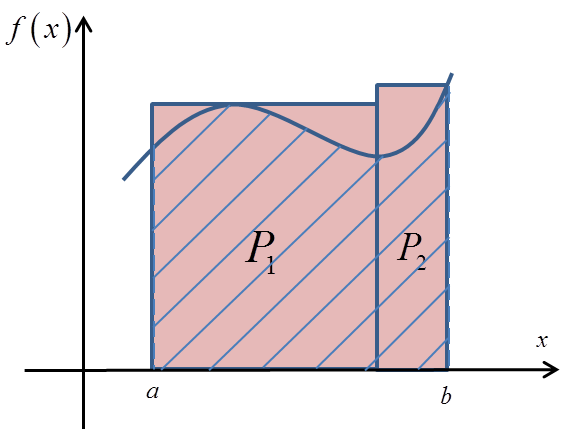
In this way we obtain a certain (probably quite rough) approximation of the area P, that is:

We can go one step further and approximate the region by the areas of three rectangles:

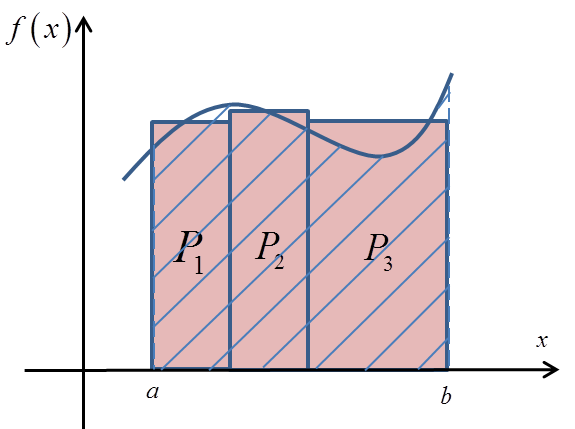
In this way we also obtain an approximation of the area P, but probably a more accurate one:

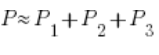
Increasing the number of rectangles to 10:

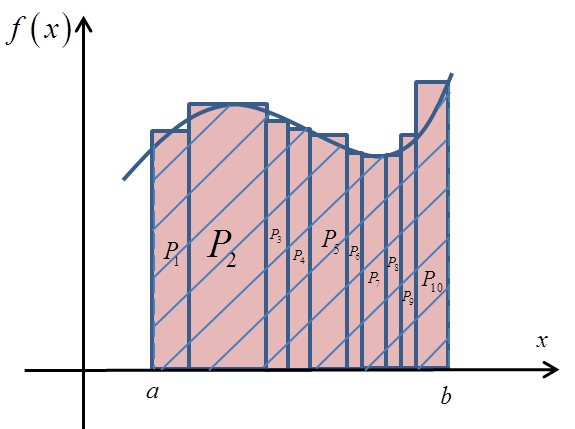
We obtain yet another, better approximation of the area P:

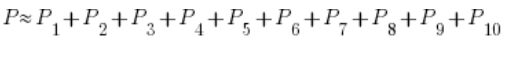
If our goal were to calculate the area P with some accuracy, we could easily achieve it by dividing it into an appropriate number of rectangles.

However, I remind you that the goal is to calculate the exact, not approximate, value of the area P. How can this be achieved?

The method is already good, only the number of rectangles must be infinite. If there are infinitely many rectangles and they are infinitely small, their sum will give us the exact value of the area P.

Simply understanding that something like this is possible pushed mathematics tremendously forward.

In this video I explain in more detail how a sum of infinitely many terms can be finite – you may treat it as a supplement to the lecture:

In this way we obtain a method to calculate the exact value of an “irregular” area. We do this by dividing it into infinitely many infinitely small rectangles and summing their areas.

The infinite sum obtained in this way (one may also say: series) is called the definite integral in the sense of Riemann (after the gentleman who first described it properly).

All that remains is to polish the formalities, which should answer several questions still hanging in the air.

We will deal with this in Part II of the Lecture.

Part II – Definition of the definite integral (as a certain series)

Let us describe in a bit more detail what we did in Part I.

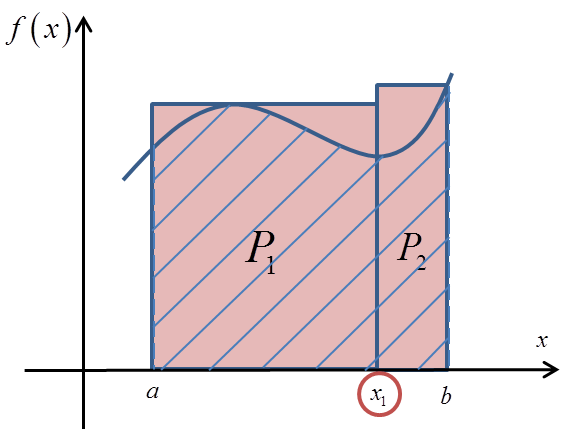
At the beginning we chose two rectangles. To do that, we had to divide the segment into two parts by a division point – say – :

What is the area equal to? Of course, side times side. The length of one side is (as you can see in the graph) . The length of the other side is the value of the function at the point , i.e. :

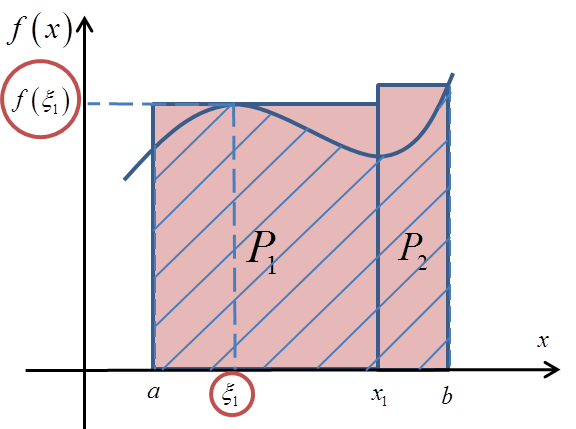
So:

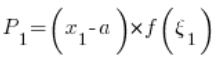
In the case of the area , one side of our rectangle has length , and our point essentially coincided with the point :

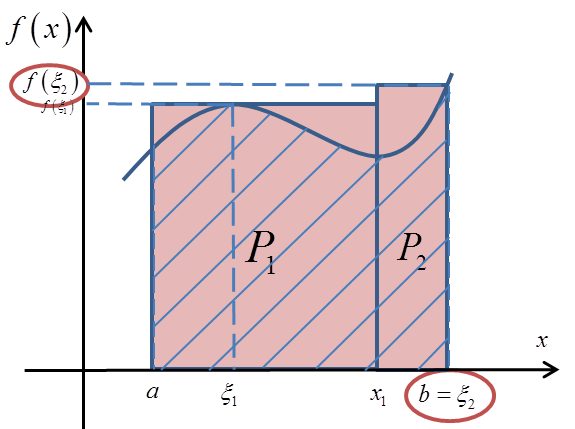
So:

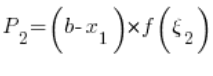
Therefore our entire area P:

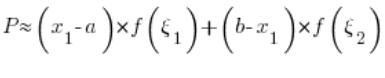
We can already sense that constructions with larger numbers of rectangles will look similar, and we will deal with that in a moment, but first let us mention a key point for the whole definition of the definite integral.

Attention.

Attention once again.

The point dividing the segment can be chosen completely ARBITRARILY. The point inside the segment could be chosen completely ARBITRARILY. The point inside the segment could be chosen completely ARBITRARILY (and we happened to take it at the endpoint of that segment).

This means that if we had adopted completely different points , , we would have obtained completely different rectangles:

However, the areas of these rectangles would still, in some way, be an approximation of the area P (of course different than last time), and by continuing our method (increasing the number of rectangles to infinity) we would still obtain the area of the region P.

Let us now approximate the area P with three rectangles, as we did in Part I.

Increasing the number of rectangles to three, we divide the segment into three parts by arbitrarily chosen points , and inside them we arbitrarily choose the points :

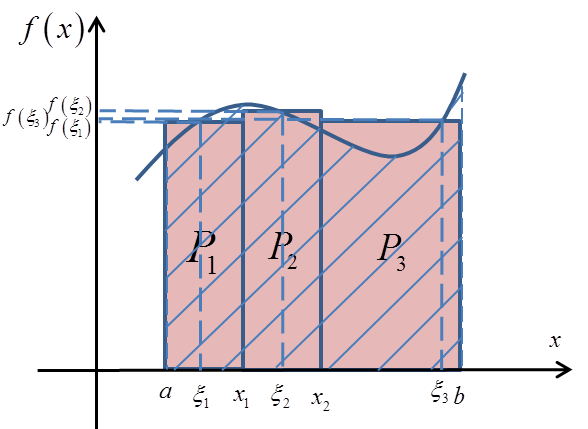
Thus obtaining an approximation of the area P:

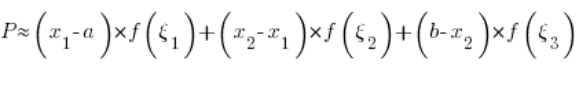
The segments: 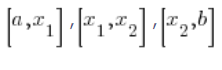can, for brevity, be denoted as:

.

So we have:

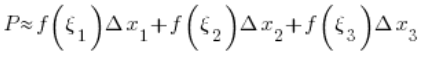
We therefore see that for any fixed partition into ‘n’ rectangles we have:

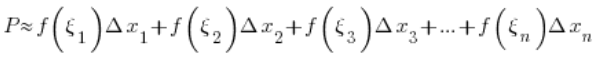
DEFINITION OF THE DEFINITE INTEGRAL

By increasing the number of subintervals into which we divide the segment to infinity, we obtain an infinite sum (called an “integral sum”):

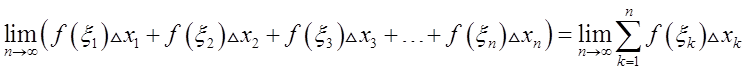
If this limit always converges to the same number, regardless of the choice of subintervals (where we assume that the lengths of these subintervals tend to zero as increases) and regardless of the choice of points , then this number is called the definite integral on the interval from a to b.

Note the non-accidental similarity of the notation:

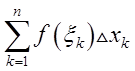
and:

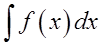
Integration is nothing other than summation. Summation of infinitely small values.

Let us once again pay attention to the important points of the definition:

• The length of the subintervals must be infinitely small, i.e. if by we denote the length of the longest of them for a given n, then it must be: . Otherwise, we could at the beginning choose some rectangle, for example , and divide the whole remaining region into infinitely small rectangles. We would then have an infinite number of rectangles, but we would not have the exact value of the area P.
• The partition of the segment into infinitely small subintervals must be completely arbitrary, as must the choice of points , and for every such choice the series must sum to the same number. If for one choice of subintervals and points we obtain a different value of the sum than for all the others, then this sum is not a definite integral.

To gain practice and a better understanding of the definition of the definite integral, in the next lecture we will move on to examples of computing definite integrals from the definition.

THE END

While writing this post I used…

1. “Differential and Integral Calculus. Volume II.” G.M. Fichtenholz. Ed. 1966.

Click here to go to the next lecture, devoted to computing definite integrals from the definition (next Lecture) –>

Click to return to the page with lectures on definite integrals