Let’s take the following sequence limit:
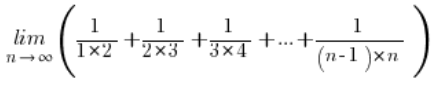
In the problem, we kind of “feel” that we need to use sequence sum formulas (arithmetic or geometric) but unfortunately, unfortunately… This sequence is neither arithmetic nor geometric…
What to do?
We have to do it completely differently. Break each fraction into simple fractions. This is done quite intensively when dealing with indefinite integrals of rational functions for example. The idea is to find constants A and B such that…
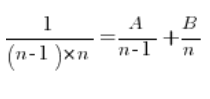
We multiply both sides of the above equation by 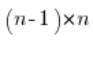 , obtaining:
, obtaining:
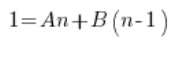
Next:
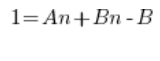
We compare the coefficients of the polynomials on the left and right sides (polynomial equality – high school) and we get a system of equations:
![]() From the second equation:
From the second equation: ![]() .
.
Substituting this into the first equation:
![]()
We also have ![]() .
.
So we can decompose any fraction into:
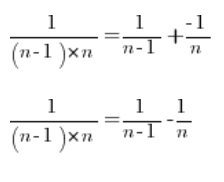
Returning to our sequence limit and decomposing each fraction into simple fractions:
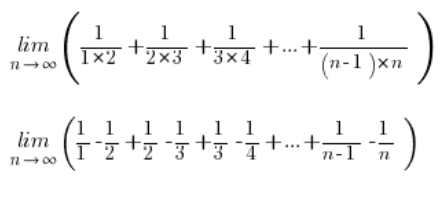
Simplifying some terms, we are left with:
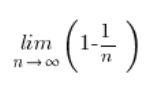
And this sequence limit is no longer scary, obviously:
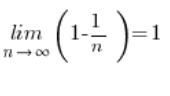
P.S.
You can find many interesting examples of sequence limits in my Video Course dedicated to limits.


