نهاية المتتالية

نهاية المتتالية – المحاضرة 1

الموضوع: نهاية المتتالية – مقدمة بديهية وتعريف

الملخص

في هذا المقال سأشرح ما هي نهاية المتتالية فعليًا، كما سأوضح بشكل أدق كيفية فهم تعريف هذه النهاية.

ما هي المتتالية؟

قبل أن ننتقل إلى شرح ما هي نهاية المتتالية، يجب أولًا أن نوضح ما هي المتتالية نفسها. المتتالية العددية هي مجموعة من الأعداد المرتبة وفق ترتيب معين، على سبيل المثال:

1، 2، 4، 7، 10

لدينا أعلاه متتالية مكوّنة من خمسة حدود. الترتيب هنا مهم. على سبيل المثال:

2، 1، 4، 7، 10

هذه متتالية مختلفة تمامًا.

عند الحديث عن نهاية المتتالية، فإننا نعمل على متتاليات غير منتهية، على سبيل المثال:

-4، -1، 2، 5، 8، 11، …

يمكن تمثيل المتتاليات إما بكتابة أول عدة حدود منها، أو – إن أمكن – بكتابة صيغة الحد العام (مثل الحد المئة). الصيغة العامة للمتتالية الأخيرة المذكورة أعلاه (-4، -1، 2، 5، 8، 11، …) تكون على الشكل التالي:

يمثل المتغير n في الصيغة رقم حد المتتالية. دعونا نتحقق من صحة ذلك:

الحد الأول من المتتالية: – صحيح (-4، -1، 2، 5، 8، 11، …)

الحد الثاني من المتتالية: – صحيح (-4، -1، 2، 5، 8، 11، …)

إلخ.

أمثلة على المتتاليات. المتتاليات المتقاربة. حدود المتتالية على المحور العددي.

يساعدنا كثيرًا في فهم معنى نهاية المتتالية تمثيل حدود المتتالية على المحور العددي بشكل بياني (وتذكر أننا من الآن فصاعدًا نتحدث دائمًا عن متتاليات غير منتهية).

لنأخذ على سبيل المثال المتتالية -4، -1، 2، 5، 8، 11، … (والتي يعطى حدها العام بالصيغة ). لو قمنا بتمثيل حدودها الأولى على المحور العددي، فسيبدو الشكل كما يلي:

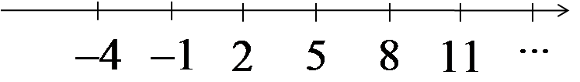
نلاحظ أنه لو قمنا بتمثيل الحدود التالية (14، 17، …) على المحور العددي فلن نقترب من أي عدد معين على المحور. بل على العكس، سنبتعد أكثر فأكثر نحو اللانهاية.

الآن متتالية أخرى:

0، -2، -4، 0، 7، 1، -2، 2، 2، …

إيجاد صيغة عامة للحد n لهذه المتتالية يكاد يكون مستحيلًا، لأن حدودها تتكوّن بطريقة عشوائية إلى حد ما ودون نمط واضح (مع أن هناك من يعتقد أن هناك دائمًا صيغة ما). لو قمنا بتمثيل هذه الحدود على المحور العددي فسنحصل على:

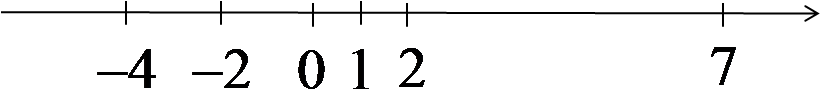
عند تمثيل الحدود المتتالية، فإنها ستقفز يمينًا ويسارًا على المحور دون أن تقترب من أي عدد. توجد مثل هذه المتتاليات أيضًا.

والآن دعونا ننظر إلى المتتالية التالية:

يمكن ملاحظة أن البسط يحتوي على الأعداد الطبيعية المتتالية، بينما المقام يحتوي على أعداد أكبر منها بواحد. الحد العام لهذه المتتالية هو . وعند تمثيل حدود هذه المتتالية على المحور العددي نلاحظ ما يلي:

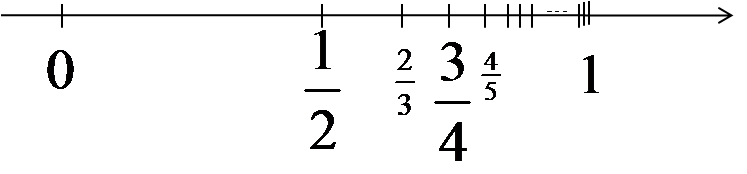
تقترب حدود هذه المتتالية أكثر فأكثر من العدد 1. على سبيل المثال، الحد المئة (يمكن حسابه بتعويض n = 100 في الصيغة ) يساوي ، وهو قريب جدًا من 1. الحد رقم 101 أقرب أكثر. الحد رقم 102 أقرب أيضًا. أما الحد الألف فهو تقريبًا يساوي 1.

كلما أخذنا أرقام حدود أكبر، اقتربنا أكثر فأكثر من الواحد. ورغم أن أي حد من حدود المتتالية لا يساوي 1 تمامًا (لأن عددًا مقسومًا على عدد أكبر منه بواحد لا يمكن أن يساوي 1)، يمكننا القول إن لهذه المتتالية نهاية تساوي 1.

ما سبق هو فهم غير رسمي وبديهي لنهاية المتتالية. لم نحدد بدقة ما المقصود بـ “أكبر فأكبر” أو “أقرب فأقرب”. سنتناول ذلك بدقة في الجزء التالي.

قبل أن نعرّف نهاية المتتالية تعريفًا صارمًا، يجب أن نراجع أمرًا مهمًا، وهو كيفية حساب المسافة بين نقطتين على المحور العددي.

صيغة حساب المسافة بين نقطتين على المحور العددي

لنأخذ محور الأعداد ونختار عليه عددين (أحدهما موجب والآخر سالب):

نحن جميعًا نعلم أن المسافة بينهما تساوي 6، ولكن كيف نحسبها بسرعة؟

يمكن القول: نطرح العدد الأصغر من العدد الأكبر. في حالتنا نطرح -4 من 2 فنحصل على . هذا صحيح. لكن قبل الطرح يجب مقارنة الأعداد لمعرفة أيها أكبر، وهذا قد يكون مزعجًا عند التعامل مع متغيرات.

لذلك يمكن اتباع طريقة أخرى: نطرح العددين بأي ترتيب ثم نأخذ القيمة المطلقة للناتج. مثلًا، نطرح 2 من -4 فنحصل على ، أو نطرح -4 من 2 فنحصل على .

إذًا، يمكن حساب المسافة بين عددين على المحور العددي باستخدام القيمة المطلقة لفارق العددين.

تعريف نهاية المتتالية

لنعد الآن إلى تعريف نهاية المتتالية.

التعريف

نقول إن العدد g هو نهاية متتالية إذا تحقق ما يلي:

\underset{\varepsilon >0}{\mathop{\forall }}\,\underset{N}{\mathop{\exists }}\,\underset{n>N}{\mathop{\forall }}\,\left| {{a}_{n}}-g \right|<\varepsilon [/latex] يمكن قراءة هذا التعريف على النحو التالي: «لكل عدد موجب ε، يوجد عدد N بحيث لكل n > N تكون المسافة بين aₙ و g أصغر من ε».

أي مهما اخترنا ε صغيرًا جدًا، يمكننا دائمًا إيجاد عدد N مناسب. وبالتالي فإن نهاية المتتالية تساوي 1.