Зведення деяких рівнянь четвертого ступеня до квадратних рівнянь
Багато поліноміальних рівнянь четвертого ступеня можна перетворити на квадратні рівняння за допомогою добре відомого зі школи трюку, описаного тут:
Зведення до квадратного рівняння
Це, звичайно, працює і для поліномів у комплексних числах.
Нагадую, мова йде про маючи рівняння:
{{z}^{4}}+3{{z}^{2}}+2=0Підставляємо: {{z}^{2}}=t
І отримуємо квадратне рівняння:
{{t}^{2}}+3{t}+2=0Далі вирішуємо його за допомогою звичайної дельти і так далі, маємо розв’язки ![]() , пам’ятаючи про те, що
, пам’ятаючи про те, що ![]() утворюємо з них два наступні рівняння:
утворюємо з них два наступні рівняння:
![]() або
або ![]()
Розв’язуємо їх і маємо чотири розв’язки: ![]() .
.
Зведення деяких рівнянь вищих ступенів до квадратних рівнянь
Абсолютно нічого не заважає розширити цей метод на рівняння вищих ступенів, ніж 4 (якщо, звичайно, їх можна звести до квадратних шляхом підстановки).
Отже, маємо:
2{{z}^{6}}-5{{z}^{3}}+4=0Можна також помітити, що це еквівалентно:
2{( {z}^{3})^{2}}-5{{z}^{3}}+4=0І після підстановки: ![]()
Виходимо на квадратне рівняння:
2{{t}^{2}}-5t+4=0У рівнянні:
{{x}^{10}}-3{{x}^{5}}+1=0Після підстановки: ![]()
Маємо:
{{t}^{2}}-3t+1=0І так далі, і так далі…
Приклад
Візьмемо рівняння:
z^6+(1-i)z^3-i=0Підставляємо z^2=t і маємо:
t^2+(1-i)t-i=0Далі рахуємо:
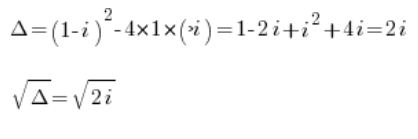
Рахуємо ці корені відомими методами комплексних чисел (показано, наприклад, у моєму Курсі).
Маємо ![]() або
або ![]()
Тобто:
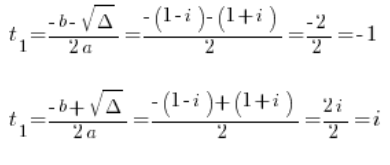
Пам’ятаючи про те, що це ще не розв’язки, бо z^3=t
Тобто маємо розв’язати рівняння:
z^3=-1А також:
z^3=iПеретворюємо їх на:
![]() та
та ![]()
І обчислюючи знову відомими методами, маємо три корені з першого рівняння:
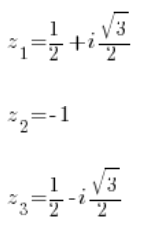
А також три корені з другого рівняння:
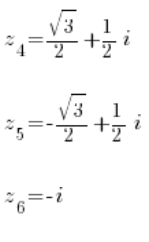
Розв’язано 🙂


