Wprowadzenie do Pochodnych Funkcji

Pochodne Funkcji Wykład 1

Temat: Intuicyjne wprowadzenie do pojęcia pochodnej funkcji (pochodna jako prędkość)

Streszczenie

W tym artykule postaram się wyjaśnić bliżej, co to w ogóle są pochodne funkcji, zaczynając zupełnie od podstaw. Do wgryzienia się w temat wystarczy ci podstawówka, kalkulator i dobre, optymistyczne  nastawienie na początku. Silnie zalecam wyposażyć się we wszystkie trzy czynniki przed lekturą!

Mały Kazio na sankach

Zaczynamy od konkretnego przykładu, na którym Ci pokażę ogólnie, co i jak z tymi pochodnymi funkcji. Wyobraźmy sobie zimę, górę i małego saneczkarza Kazimierza, zjeżdżając ze szczytu górki. Wszyscy znamy taki zjawisko, że na początku sanki suną bardzo powoli, a później lecą coraz szybciej rozpędzając się (zakładając optymalny, bezpieczny dla Małego Kazika przebieg jazdy). Wyobraźmy też sobie, że w celu opisu jazdy sankami co sekundę bardzo dokładnie badamy drogę przebytą przez sanki. Weźmy pomiary odległości dla pierwszych sześciu sekund ruchu sanek:

Z analizy tabelki “mamy na piśmie” to, co każdy intuicyjne wyczuwa, to znaczy to, że sanki nie poruszają się jednostajnie. W pierwszej sekundzie ruchu mały Kaziu przejechał (można tak powiedzieć o sankach?) tylko pół metra, a na przykład między pomiarem w drugiej, a trzeciej sekundzie przejechał 2,5 metra w tym samym czasie. Na początku sanki musiały więc sunąć powoli, a później coraz szybciej. Pochodne funkcji związane są ściśle z prędkością.

Nanieśmy nasze pomiary na wykres (tu przydadzą się cenne wiadomości z podstawówki):

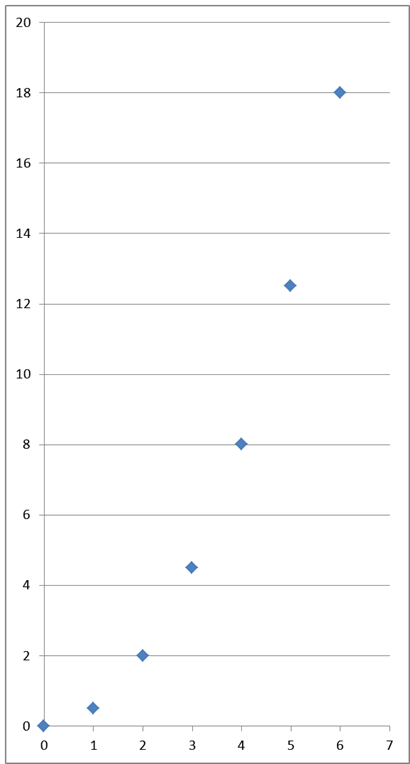
Poświęć chwilę, żeby powiązać wykres z tabelką. Da się zauważyć pewną regularność kropek, prawda? Było to raczej ciężkie do zauważenia na samych liczbach w tabelce, dlatego graficzne przedstawianie różny operacji algebraicznych jest w matematyce bardzo ważne, niektórzy (Kartezjusz) starali się nawet całą matematykę sprowadzić do geometrii! Wracajmy jednak do pochodnych funkcji.

Zależność drogi od czasu (przy okazji taką zależność nazywamy funkcją – na pochodne funkcji trzeba jeszcze będzie cierpliwie poczekać) nie jest w naszym modelu zupełnie przypadkowa. Przyjrzyj się uważnie tabelce. Co mają wspólnego liczby oznaczające czas (0,1,2,3,4,5,6…) i odpowiadające im liczby oznaczające przebytą drogę (0;0,5;2;4,5;8;12,5;18…) ?

Jeżeli odpowiedziałeś prawidłowo, że liczby 0;0,5;2;4,5;8;12,5;18… są połówkami kwadratów liczb 0,1,2,3,4,5,6… to jesteś bardzo dobry w te klocki, gratuluję! Spójrz, przyjrzyjmy się każdej kolumnie po kolei:

0 (droga) równe jest połowie kwadratu zera (czas) – zgadza się

0,5 (droga) równe jest połowie kwadratu 1 (czas), bo – zgadza się

2 (droga) równe jest połowie kwadratu 2 (czas), bo – zgadza się

4,5 (droga) równe jest połowie kwadratu 3 (czas), bo – zgadza się

8 (droga) równe jest połowie kwadratu 4 (czas), bo – zgadza się

12,5 (droga) równe jest połowie kwadratu 5 (czas), bo – zgadza się

18 (droga) równe jest połowie kwadratu 6 (czas), bo  – zgadza się.

Można powiedzieć, że droga z czasem związana jest zależnością droga=(czas^2):2, a jeżeli przyjmiemy za drogę s, a za czas t matematycznym wzorem: . Żeby poczuć się bardziej swojsko, przyjmijmy za zmienną zależną od drugiej (drogę) literkę y, a za zmienną niezależną (czas) literkę x. Otrzymamy wtedy wzór opisujący ruch sanek w pierwszych sześciu sekundach:

Taką funkcję można nazwać wielomianem drugiego stopnia. W czasach, kiedy powstawało pojęcie pochodnej (albo kiedy odkrywano pojęcie “pochodne funkcji” – zależnie jaką filozofię matematyki przyjąć) właśnie przy pomocy wielomianów opisywano wiele konkretnych zjawisk fizycznych – naporu wody na tamy, toru lotu pocisku artyleryjskiego, ruch gwiazd i planet. Coraz większa złożoność problemów związanych z różnorodnymi zastosowaniami matematyki wywołały duże parcie na znajdywanie coraz lepszych i bardziej szczegółowych metod analizy funkcji – proste dodawanie, czy mnożenie już nie wystarczało. Różni uczeni w różny sposób małymi kroczkami i odkryciami zbliżali się do pojęcia pochodnej funkcji, do którego my również zaraz dojdziemy 🙂

I Ty również, jeśli w swojej karierze zawodowej np. inżyniera, czy ekonomisty, planujesz wyjście poza – powiedzmy – XVII wiek w rozwoju wiedzy ludzkości musisz przejść tą drogę – tutaj skrótów nie ma.

Ciągłość funkcji

Przyjrzyjmy się jeszcze raz naszej tabelce. Jako model opisujący ruch saneczek daleko jej do doskonałości. Czy jeżeli nie ma w niej żadnej wartości dla czasu 2,5 sekundy oznacza to, że w 2,5 sekundzie ruchu sanki nie przebyły żadnej drogi? Że sanki między drugą a trzecią sekundą ruchu przeteleportowały się z drugiego metra na czwarty? Oczywiście nie. W 2,5 sekundzie ruchu sanki również przebyły pewną drogę, tylko po prostu nie zmierzyliśmy jej, tak samo jak 2,99999 sekundzie ruchu i w ogóle dla każdej wartości czasu oprócz zera sanki przebyły pewną drogę.

Jaka mogła by być to droga?

Skoro wiemy już, że droga związana jest z czasem zależnością (gdzie y to droga, a x to czas) możemy to łatwo policzyć, podnosząc 2,5 do kwadratu i dzieląc wynik przez 2. Matematycznie można zapisać:

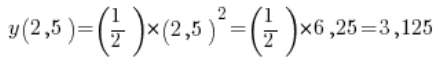
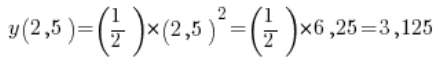
Gdyby wartość tą zaznaczyć na naszym wykresie, otrzymalibyśmy:

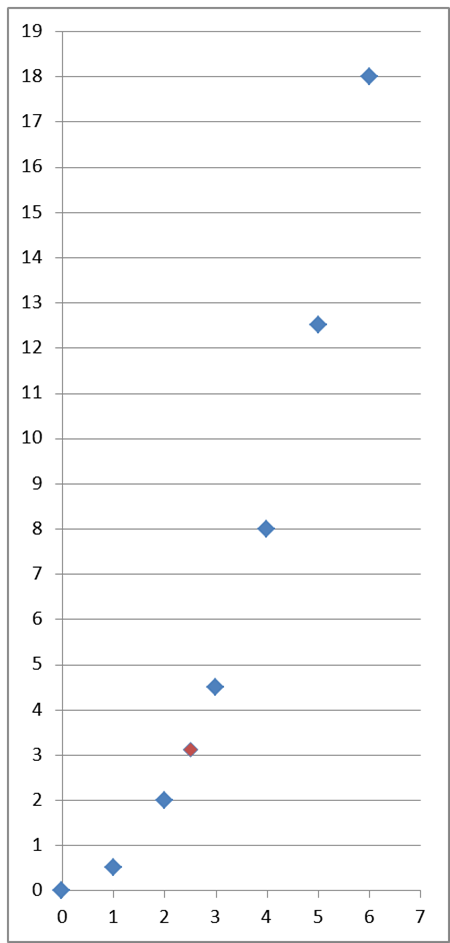
Jasnym jest, że odpowiednią wartość drogi moglibyśmy obliczyć także w 0,0001 sekundzie ruchu, i w ogóle w każdej. Dla każdej z nich moglibyśmy nanieść odpowiednią kropkę. Wszystkie te kropki zaś połączyły by nam się w elegancki wykres:

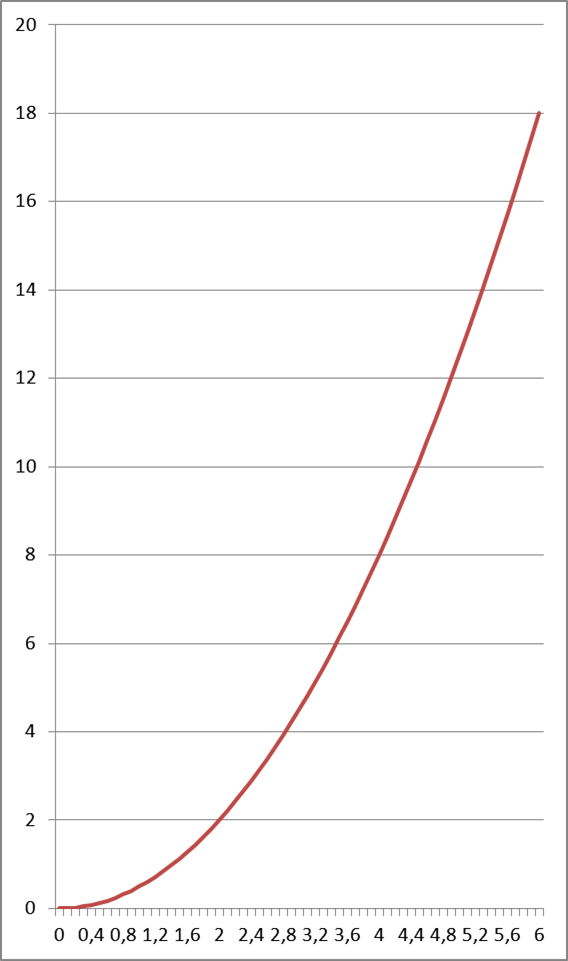
Funkcje takiego typu, w których dla każdej liczby x z pewnego przedziału (w naszym przypadku od 0 d0 6), także dla x-sów będących ułamkami, lub liczbami niewymiernymi (np. ), istnieje wartość y możemy nazwać funkcjami ciągłymi. Funkcje ciągłe na wykresach łączą się w ładne linie, które można narysować bez odrywania długopisu od kartki. Czas jest klasycznym przykładem wartości ciągłej. Możemy mówić o 1,9999999 sekundzie ruchu, albo o sekundzie ruchu. Można też przyjąć, że wzrost jest wartością ciągłą – nie ma problemu, żeby człowiek miał 176,000002 cm wzrostu. Dla odmiany – np. liczba dzieci w rodzinie nie jest wartością ciągłą, bo nie można mieć 2,49837 dzieci. Dochodzimy tu do ważnej rzeczy:

Pochodne funkcji dotyczą się tylko funkcji ciągłych.

Pojęcie prędkości zmiany

Mamy więc funkcję opisującą zmianę drogi przebytą przez małego Kazia pod wpływem czasu i narysowany jej wykres. Wróćmy do zjawiska , o którym mówimy już od samego początku – to znaczy do prędkości. Na początku dla zmian czasu droga przebyta przez sanki rosła powoli. Po kilku sekundach dla takich sam zmian czasu ta droga rosła o coraz większe wartości. Przyjrzyj się wykresowi, widać tam to wyraźnie. Tym jest właśnie prędkość, prawda? Jest to miara zmiany drogi względem czasu.

Jak zmierzyć prędkość sanek w dowolnej chwili ich drogi w tak opisanym ruchu? Nie mamy prędkościomierza, przypominam (jesteśmy w XVII wieku). Masz jakieś pomysły na tym etapie?

Jak mierzyć prędkość? Prędkość średnia

Fajnym pomysłem na pomiar wielkości zmiany drogi względem czasu jest po prostu podzielenie jednego przez drugie. Jeżeli drogę – np. 400 km (zostawmy na chwilę te sanki) przejedziemy w 5 godzin, to jako wynik otrzymamy liczbę przejechanych kilometrów na 1 godzinę, czyli 400 przez 5 będziemy mieli 80. Oznacza to, że jechaliśmy całą drogę średnio .

Oczywiście, ta miara (prędkość średnia) nie przekazuje informacji o tym, ile grzaliśmy po drodze na autostradzie, czy robiliśmy sobie postoje i z jaką prędkością sunęliśmy w korkach przejeżdżając przez duże miasta. Nie jest to więc jeszcze to, o co nam chodzi.

Wracając do naszego saneczkarskiego przykładu na pochodne funkcji:

W ciągu 6 sekund mały Kaziu przejechał 18 metrów (możemy wyczytać to z tabelki). Daje to nam średnią prędkość jego ruchu: 18:6=3 metry na sekundę. A jak obliczyć, z jaką prędkością jechał Kazimierz w 2 sekundzie zjazdu sankami? Z pewnością nie były to 3 metry na sekundę… Czy takie pytanie w ogóle ma sens? Z życia wiemy, że tak – ale jak to w ogóle policzyć, znając tylko pojęcie prędkości średniej? Jakie przyrost drogi i jaką zmianę czasu przyjąć i co przez co podzielić? Wyciągaj kalkulator i policz trochę ze mną…

Chcemy obliczyć prędkość sanek w 2 sekundzie ruchu.

Obliczmy najpierw prędkość średnią (to już umiemy) sanek między 2 a trzecią sekundą ruchu.

Droga przejechana między drugą a trzecią sekundą to: 4,5 (droga przejechana w 3 sekundzie) – 2 (droga przejechana w drugiej sekundzie) = 2,5. Zatrzymaj się tu chwilkę. To musi być dla Ciebie całkowicie jasne.

Czas pomiędzy drugą a trzecią sekundą to oczywiście 1 sekunda. Dzieląc jedno przez drugie otrzymamy: .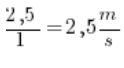

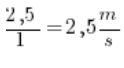
Czyli pomiędzy drugą a trzecią sekundą sanki mknęły z prędkością .

Obliczmy teraz prędkość średnią sanek między 2 a 2,5 sekundą ruchu.

Jaką drogę przebyły sanki w 2,5 sekundzie ruchu? Liczyliśmy już wcześniej, policzymy jeszcze raz. Skoro droga równa jest czasowi do kwadratu podzielonemu przez dwa, wystarczy 2,5 podnieść do kwadratu i podzielić przez 2. Zachęcam do użycia kalkulatorka, wyjdzie nam: 3,125.

Droga przejechana między 2 a 2,5 sekundą będzie więc: 3,125 (droga przejechana w 2,5 sekundzie) – 2 (droga przejechana w drugiej sekundzie) = 1,125.

Czas pomiędzy 2 a 2,5 sekundą to – uwaga – 0,5 sekundy! Dzieląc jedno przez drugie otrzymamy (użyj kalkulatora): .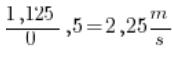

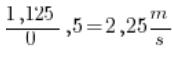
Czyli pomiędzy 2 a 2,5 sekundą sanki miały już  prędkość mniejszą (po zastanowieniu – to logiczne, prawda?), bo  .

Które obliczenie prędkości średniej wydaje Ci się bliższe dokładnej prędkości w 2 sekundzie ruchu? Prędkość średnia pomiędzy 2 a 3 sekundą, czy pomiędzy 2 a 2,5 sekundą? Oczywiście ten drugi. Widać, do czego zmierzamy?

Weźmy teraz prędkość średnią sanek między 2 a 2,25 sekundą ruchu.

Jaką drogę przebyły sanki w 2,25 sekundzie ruchu? 2,25 podnosimy do kwadratu i dzielimy przez 2 (kalkulator). Wyjdzie nam: 2,53125.

Droga przejechana między 2 a 2,25 sekundą będzie więc: 2,53125 (droga przejechana w 2,5 sekundzie) – 2 (droga przejechana w drugiej sekundzie) = 0,53125.

Czas pomiędzy 2 a 2,25 sekundą to 0,25 sekundy. Dzieląc jedno przez drugie otrzymamy (użyj kalkulatora): .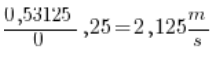

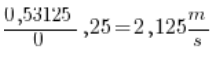
Teraz prędkość średnią sanek między 2 a 2,1 sekundą ruchu.

Droga w 2,1 sekundzie ruchu = 2,205.

Droga między 2 a 2,1 sekundą = 2,205 – 2 = 0,205.

Czas pomiędzy 2 a 2,1 sekundą to 0,1 sekundy. Dzieląc jedno przez drugie: .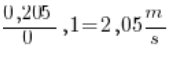

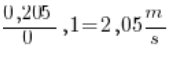
Licząc analogicznie prędkości pomiędzy 2 a 2,05 sekundą otrzymamy wynik:

Pomiędzy 2 a 2,01 sekundą: .

Pomiędzy 2 a 2,001 sekundą:

Mamy więc kolejne przybliżone prędkości średnie, z których każda z nich jest coraz bliższa dokładnej prędkości w 2 sekundzie ruchu:

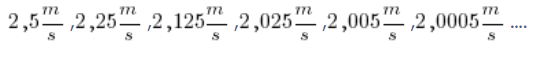
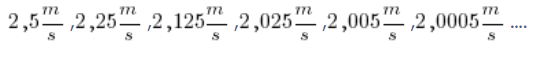
Oczywiście nie trzeba tu Einsteina, żeby zauważyć, że te wartości są coraz bliższe . Inżynierowie i uczeni w XVI – XVII wieku stosowali tego typu metodę przybliżeń, aż uzyskiwali wystarczające przybliżenie do tego, żeby tama nie pękła, budynek się nie zawalił, a statek dopłynął do celu.

Pochodne funkcji w punkcie

Biorąc więc kolejne przybliżenia jak wyżej, uzyskujemy coraz dokładniejszy pomiar prędkości. Kiedy uzyskamy już odpowiednie przybliżenie, możemy proces zakończyć. Spróbujmy teraz trochę sformalizować to, co robiliśmy powyżej. Badaliśmy prędkość w drugiej sekundzie ruchu. Oznaczmy . Najpierw obliczaliśmy odpowiednie odcinki dróg przebyte w kolejnych odcinkach czasu, na przykład od drogi w trzeciej sekundzie odejmowaliśmy drogę w drugiej. Zwróć uwagę, że jeśli przyrosty czasu (najpierw 1 sekunda, potem pół sekundy, potem 0,25 sekundy itd) oznaczymy jako   , to odpowiadające im przyrosty drogi można oznaczyć jako: , gdzie  oznacza drogę przebytą w 3; 2,5; 2,25 sekundzie i tak dalej, a – drogę w drugiej sekundzie.

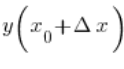
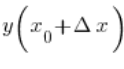
Kolejne prędkości średnie obliczaliśmy ze wzoru:

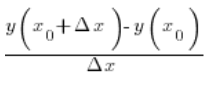
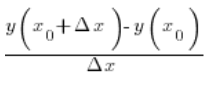
Później braliśmy coraz mniejsze i mniejsze wartości . Intuicyjnie wyczuliśmy, że tak uzyskane wartości “dążą” do 2 – bez formalnego oznaczania, co te “dążą” ściśle znaczy. Może trudno w to uwierzyć, ale takie intuicyjne posługiwanie się rachunkiem na nieskończonościach (a konkretnie wartościach nieskończenie małych) zupełnie wystarczało przez wiele, wiele lat. Na formalne i ścisłe zdefiniowanie pochodne funkcji czekały jeszcze wiele lat. Tą operację, czyli sprawdzanie do czego wyrażenie “dąży” można zapisać jako:

– czyli jako granicę (“limes”), do której “zbliża się” wyrażenie przy “zbliżającym się” do zera.

Nadszedł czas na długo już chyba oczekiwane pochodne funkcji. Pochodne funkcji w punkcie można opisać właśnie taką granicą:

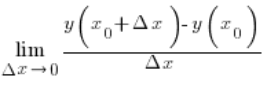
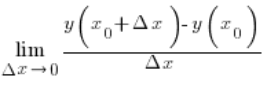
Czy to znaczy, że mechaniczna prędkość w jakiejś chwili (np. ruch sanek, samochodu, roweru, klocka na pochylni) to właśnie pochodna funkcji w punkcie? Dokładnie tak. Ale pojęcie to jest o wiele szersze i nie musi ograniczać się do analizy mechanicznej ruchu.

Pochodne funkcji w zastosowaniach

We wzorze na pochodne funkcji w punkcie dzielimy przyrost wartości funkcji (y-ków) przez przyrost argumentów funkcji (x-sów). Otrzymujemy więc jako wynik to ile razy przyrost wartości funkcji jest większy od przyrostu argumentów. Czyli otrzymujemy pewną miarę “jak szybko” rośnie wykres jakiejkolwiek funkcji, niekoniecznie opisującej ruch jakiś obiektów fizycznych. Może to być przyrost temperatury, ciśnienia, wskaźnika optymizmu konsumentów, czy kursów na giełdzie! Możliwości są nieskończone, bo tylko to sobie wyobraź – wszystko co się zmienia, może zmieniać się z różną prędkością. A jeśli chcemy badać tą prędkość w sposób ścisły, a nie tylko “mniej więcej”, musimy użyć właśnie pochodnych.

Często bywa odwrotnie – znamy prędkość zmian, a nie znamy funkcji, opisującej zmiany – wtedy wejść musimy w operację odwrotną do obliczania pochodnej –  czyli całkę.

Pochodne funkcji jako inne funkcje

W przykładzie z saneczkami badaliśmy pochodną w konkretnym punkcie {{x}_{0}}=2i otrzymaliśmy konkretną wartość 2. Nietrudno sobie wyobrazić, że tak samo moglibyśmy badać pochodne funkcji w każdym innym punkcie {{x}_{0}}=1, {{x}_{0}}=0,5, albo {{x}_{0}}=4. Otrzymane wartości pochodnych również nie były by zupełnie chaotyczne (zapraszam Cię zresztą, żebyś je sobie policzył), ale ułożyły by się w funkcję , czyli pochodna w punkcie {{x}_{0}}=1wyszła by równa 1 itd.

Co to oznacza? Otrzymując pochodną w jakimś punkcie równą 10 wiemy, że w tym punkcie przyrost wartości funkcji jest 10 razy większy od przyrostu argumentów wykres rośnie bardzo ostro do góry, a zjawisko opisywane przez funkcję zmienia się szybko. Jeżeli pochodna wyjdzie równa np. , zmiana nie następuje zbyt szybko.

Pochodne funkcji w dowolnym punkcie, a nie w jakimś konkretnym liczymy ze wzoru (z definicji):

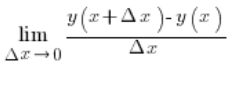
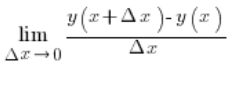
Jako wynik otrzymamy oczywiście inną funkcję. Dla ułatwienia obliczeń możemy użyć też wzorów i właściwości pochodnych.

KONIEC

Kliknij, aby zobaczyć, jak inaczej zrozumieć można pochodne funkcji (następny Wykład) –>

Kliknij, aby wrócić na stronę z Wykładami do pochodnych