Do odpowiedzi na postawione w tytule pytanie nie potrzebujemy sięgać aż do definicji asymptoty ukośnej, wystarczy nam sama wiedza o tym, czym jest funkcja.
Jak często w matematyce bywa – wyobrazimy sobie roboczo, że wykres funkcji MA dwie różne asymptoty ukośne przy 
i pokażemy, że przyjmując takie założenie dojdziemy na pewno do sprzeczności, zatem tego założenia przyjąć nie można.
Wykres
Na wykresie te asymptoty mogły by wyglądać na przykład tak:
A wykres funkcji powinien zbliżać się do tych asymptot przy , zatem wyglądać będzie następująco:
I co? Może tak być? Czy tak wyglądać może wykres funkcji? Czy jednak mamy tu jakiś problem?
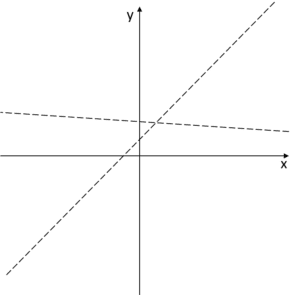
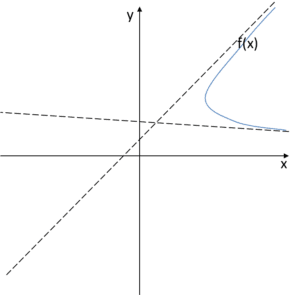
Problem
Oczywiście mamy. To, co jest powyżej nie może być wykresem funkcji. Sięgnijmy do źródeł, funkcja z definicji to przyporządkowanie, które każdemu argumentowi x przyporządkowuje dokładnie jedną wartość y. A co wynika z naszego wykresu?
Odczytać można z niego, że na przykład argumentowi 
przyporządkowane są dwie wartości – 
i 
. A tak nie może być w wykresie funkcji, bo w niej każdemu argumentowi x odpowiadać musi tylko jedna wartość y.
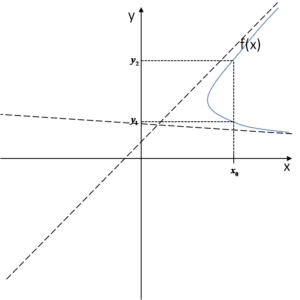
Zatem funkcja nie może mieć dwóch różnych asymptot ukośnych przy . Całe rozumowanie można powtórzyć odpowiednio dla 
🙂
4 Komentarzy
E
Przy tych asymptotach może istnieć funkcja, tylko inna.
Krystian Karczyński
Tak, przy do dwóch asymptot ukośnych mogą dążyć dwa osobne wykresy dwóch osobnych funkcji.
Ale wykres jednej funkcji może mieć tylko jedną asymptotę ukośną przy [pmath]x{right}{+\infty}[/pmath] i jedną przy [pmath]x{right}{-\infty}[/pmath]
ada
czy jeśli nie mamay asymptoty pionowej to liczymy dalej??
Krystian Karczyński
Tak. Jak nie ma pionowej, to liczymy dalej. Jak jest, to zresztą też 🙂 Pionowe w ogóle nie mają nic do ukośnych.