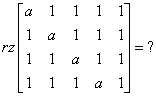
Rząd macierzy z parametrem
Krystian Karczyński
Założyciel i szef serwisu eTrapez.
Magister matematyki Politechniki Poznańskiej. Korepetytor matematyki z wieloletnim stażem. Twórca Kursów eTrapez, które zdobyły ogromną popularność wśród studentów w całej Polsce.
Mieszka w Szczecinie. Lubi spacery po lesie, plażowanie i kajaki.
Weźmy do policzenia rząd macierzy:
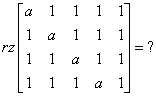
Rozwiązanie
Można się za to zabrać na klika sposobów, a najszybciej chyba będzie pomnożyć piątą kolumnę przez -1 i dodać do pierwszej, drugie, trzeciej i czwartej, uzyskując w ten sposób:
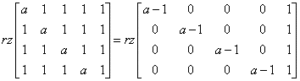Weźmy teraz wyznacznik macierzy 4-tego stopnia:
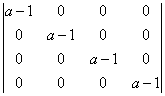Wyznacznik, którego wszystkie elementy poza główną przekątną są równe 0 jest równy iloczynowi elementów na głównej przekątnej (kiedyś to jeszcze wykażę któregoś dnia 🙂 ), zatem:
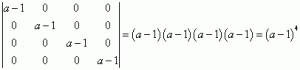Wyznacznik ten jest różny od zera dla wszystkich a różnych od 1. Zatem dla takich a rząd naszej macierzy, który mamy obliczyć równy będzie 4 (bo można z niej wyodrębnić niezerowy minor 4 stopnia, a większego już się nie da).
A co z przypadkiem, w którym 
. Uzyskamy wtedy rząd macierzy (wstawiam za a jedynkę):
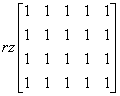A ten rząd równy jest 1 (można np. znowu podziałać piątą kolumną na pozostałe i wykreślić zerowe kolumny).
Zatem dla a różnego od 1 rząd macierzy równy jest 4, a dla a równego 1 rząd macierzy równy jest 1.
Jedna z wielu opinii o naszych Kursach...
Zakupiłem cały pakiet kursów mimo, że już dobijam do wieku emerytalnego i jestem po studiach technicznych. Nie znaczy to jednak , że zainteresowanie matematyką osłabło. Wręcz przeciwnie! Jestem w trakcie ich „konsumowania”. Mogę stwierdzić jedno – to co robicie jest fantastyczne. Pomoc dla wszystkich, czy to uczniów szkół ponadpodstawowych czy też dla studentów. To nie są pieniądze wyrzucone w błoto!Aleksander M.
Szukasz korepetycji z matematyki na poziomie studiów lub szkoły średniej? A może potrzebujesz kursu, który przygotuje Cię do matury?
Jesteśmy ekipą eTrapez. Uczymy matematyki w sposób jasny, prosty i bardzo dokładny - trafimy nawet do najbardziej opornego na wiedzę.
Stworzyliśmy tłumaczone zrozumiałym językiem Kursy video do pobrania na komputer, tablet czy telefon. Włączasz nagranie, oglądasz i słuchasz, jak na korepetycjach. O dowolnej porze dnia i nocy.
Jak dla mnie, to zbyt prosty przykład został omowiony, bo nie bylo zadnego kombinowania
Witam a co zrobić w takim przypadku gdy![delim{[}{matrix{2}{3}{a 1 5 {-1} 1 5}}{]}](data:image/gif;base64,R0lGODlhAQABAAAAACH5BAEKAAEALAAAAAABAAEAAAICTAEAOw== "delim{[}{matrix{2}{3}{a 1 5 {-1} 1 5}}{]}")
?
Witam
Trochę poprawiłem formułę, mam nadzieję, że jest tak, jak miało być.
Można np. pomnożyć pierwszy wiersz przez -1 i dodać do drugiego. Wyjdzie rząd macierzy równy 1 dla a=-1, lub rząd macierzy równy 2 dla a -1.
Tak właśnie o to mi chodziło i a w tym przypadku należy do rzeczywistych. Dziękuje bardzo ja takiego typu mam zadanie na egzaminie na 5:).
Bardzo dobre kursy niemal wszystko zostaje w głowie po uważnym przesłuchaniu lekcji 🙂
Szkoda że tak późno wpadłem na te kursy i teraz cała noc trzeba siedzieć:)
Polecam warto skorzystać z kursów
Witam.
Jutro mam koło z przestrzeni liniowych i chciałbym pana prosić o wytłumaczenie zadania ze strony , którą podał Krzysiek.
Czy może Pan jakoś wytłumaczyć temat pt. macierz przekształcenia liniowego ? np. nie wiem skąd wziąć wartość na wektorach bazowych proszę o pomoc!
Cholera, to wydaje się takie proste, jeżeli się nad tym zastanowisz.