Granica ciągu Wykład 3
Temat: Wyrażenia nieoznaczone
Streszczenie
W artykule przybliżę, czym są wyrażenia nieoznaczone pojawiające się w zadaniach na granicę ciągu.
Łatwe do wyznaczenia granice ciągu
Jak obliczać granice ciągu? Jeśli zetknąłeś się z tym tematem na studiach, albo gdzie indziej, z pewnością kojarzy Ci się on z metodami, wyciąganiem przed nawias, mnożeniem przez sprzężenie itd. I słusznie. Ale wiele ciągów ma tak prostą do obliczenia granicę, że korzystanie z jakiś złożonych metod w najlepszym razie jest stratą czasu i wysiłku.
Przykład 1
Przeanalizujmy ciąg:
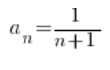
Kolejne wyrazy ciągu wyglądały by tak:
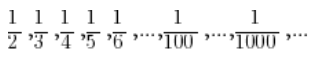itd.
Widzimy, że jego wyrazy są coraz mniejsze, mniejsze i dążą do zera. Po zastanowieniu można dojść do wniosku, że podobny wynik granicy otrzymamy w każdej sytuacji, w której licznik zmierzać będzie do stałej liczby, a mianownik rozbiegać w nieskończoność. Granica równa będzie wtedy zawsze zero – bo przy coraz większym i większym mianowniku całe wyrażenie będzie coraz mniejsze i mniejsze – dążące do zera. Zatem:
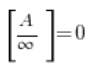
…niezależnie od tego, jaki konkretnie ciąg jest na dole w mianowniku, jeśli tylko rozbiega do nieskończoności.
Kiedy będzie to wyglądało inaczej?
Wyrażenia nieoznaczone typu 
Przykład 2
Weźmy dwa ciągi: 
. Oba rozbiegają w nieskończoność. Jeśli podzielimy ich odpowiadające sobie wyrazy otrzymamy nowy ciąg:
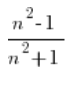
Symbolicznie taką sytuację oznaczamy 
– jest to oznaczenie na ciąg złożony z dzielenia dwóch innych rozbiegających w nieskończoność. Jaka będzie jego granica?
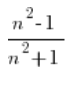
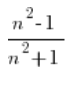
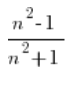
Rozpisując otrzymamy:
Te liczby zbliżają się coraz bardziej do jeden. Dla tego konkretnego ciągu więc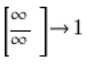 
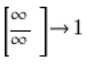
Przykład 3
Weźmy sobie dwa inne ciągi: 
. Oba rozbiegają w nieskończoność. Dzieląc ich wyrazy otrzymamy następujący ciąg:
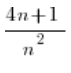
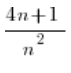
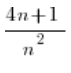
Jest to ciąg, w którym znowu w liczniku i mianowniku mamy ciągi rozbiegające w nieskończoność, a zatem znowu sytuację . Jaka jednak tym razem będzie jego granica?
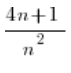
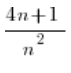
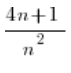
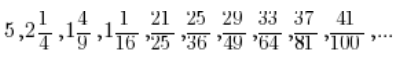
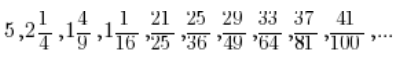
Rozpisując kolejne wyrazy ciągu otrzymamy:
Czyli zauważyć można, że mianownik rozbiega jakby “szybciej” do nieskończoności od licznika, a całe wyrażenie dąży do 0.
W obu przykładach (2 i 3) mieliśmy tą samą sytuację: i dwa różne wyniki: 1 i 0. Nietrudno wyobrazić sobie różne inne możliwości, na przykład licznik rozbiegający “szybciej” od mianownika – wtedy ciąg rozbiegał będzie w nieskończoność.
W sytuacji nie jesteśmy więc w stanie określić na samym starcie, jaka jest granica ciągu i trzeba w niej stosować różne przekształcenia wyrażenia, z którego liczymy granicę.
Wyrażenia nieoznaczone ogólnie
Tego typu wyrażenia nazywamy “symbolami nieoznaczonymi” (jest ich w sumie siedem). Policzenia granicy ciągu z symboli nieoznaczonych wymaga użycia różnych metod, natomiast jeśli w ciągu wyrażenia nieoznaczone nie występują – jest to na ogół ciąg, którego granicę wyznaczyć bardzo prosto.
Wypiszmy więc wszystkie symbole nieoznaczone:
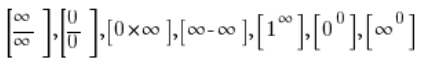
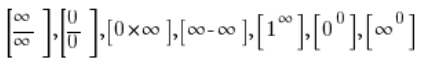
Ważną rzeczą jest zrozumienie tego, że wyrażenie nieoznaczone jest pewnym symbolem, które niesie treści różne od tych, do których się może przyzwyczailiśmy. Na przykład symbol 
w wyrażeniach nieoznaczonych NIE oznacza liczby zero (jak wielu ludziom się błędnie wydaje…) tylko ciąg o granicy równej zero – a to zupełnie coś innego, prawda? W symbolu 
nie mamy więc “dzielenia przez zero”, tylko iloraz dwóch ciągów dążących do zera.
Kliknij, aby przypomnieć sobie, jak liczyć granice ciągu z definicji (poprzedni Wykład) <–
Kliknij, aby poznać definicję granicy niewłaściwej ciągu (następny Wykład) –>
moje dziecko dostało zadanie
2 x … = Nieskończoność
czyli : dwa razy (jakaś cyfra) równa się nieskończoność
czy ktoś poradzi?
Czy to wyrażenie jest granicą? To już jakieś końcowe przekształcenia, czy fragment jakiegoś zadania?
Trudno mi określić jednoznacznie, ale jeśli mamy równanie (raczej w granicy)
2*coś=nieskończoność
to x jest liczbą dążącą do nieskończoności.
Witam, jak obliczyć granicę n³/2^pierwiastek z n?
Witam, jak obliczyć granicę \lim _ { n \rightarrow \infty } \frac { n ^ { 3 } } { 2 ^ { \sqrt { n } } }
Witam zrobi pan zadanie z kursu pochodne lekcja 4?
Robię ze wzoru 
potem robię oddzielną granice i mam 
no i co mam z tym z zrobić?
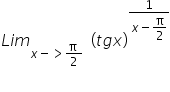
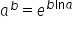
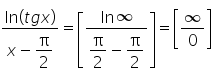
Witam, jak należy zabrać się za granicę takiego typu?
Pozdrawiam!
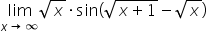
Witam, mam zadanie obliczyć granice bez użycia pochodnych. Czy to możliwe. Na Pana kursach w ogóle nie są poruszane takie zagadnienia, albo nie mogę ich znaleźć.
Czy może Pan pomóc mi w tym??
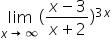
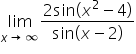
również mam problem ponieważ mam granice lim x->oo (2x^2 +1)^453 /2^450 *(x^3+3n)^302 . nie mam pomyslu na ta granice
Mam nadzieję, że dobrze zrozumiałem i mamy tu na myśli granicę
. W takich przykładach trzeba umiejętnie “wyłowić” to co istotne. Tutaj x zbiega do nieskończoności zatem to będzie najważniejszy punkt, trzeba standardowo wyłączyć przed nawias x w najwyższej potędze co krok po kroku postaram się zrobić:
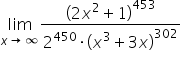
Po drodze skorzystałem z własności potęg
, skróciłem 
a pod koniec 
gdy 
.
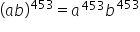
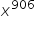
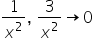
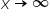
Witam mam problem z pewną granicą, a mianowicie chodzi o policzenie as. poziomych dla (x^2/e^x). W obu wychodzi symbol nieoznaczony i co należy dalej zrobić?
ja mam takie dość durne zadanie na kolosa i za bardzo nie mam pomysłu jak sie za to zabrac
jakieś propozycje
Najgorsze są właśnie te różne potęgi i nie wiem jak sie ich wyzbyć
Witam
Granicę z potęgami najczęściej rozwiązujemy zapisując wszystkie liczby do potęgi n tzn. jeśli przykładowo w granicy pojawia się
to rozpisujemy to jako 
. Następnie dzielimy licznik i mianownik przez najwyższą potęgę z mianownika, mam tu na myśli potęgi liczb np. 
itd. Trzeba mieć świadomość, że wyrażenia tego typu dążą “szybciej” do nieskończoności niż wyrażenia typu 
itd. Tym samym granicę podaną przez Pana można rozwiązać następująco:
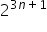
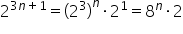
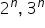
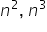
Dalej ponieważ
oraz 
(jak wcześniej wspomniałem mianownik dąży tu do zera “szybciej” niż licznik!) dostajemy
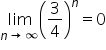
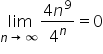
nie wiem jak obliczyć granicę z n!/n czy jest to jakiś wyjątek?
Witam ,czy symbol oo^0 zawsze będzie dawał 1
Przepraszam czy mógłby mi pan pomóc w pewnym zagadnieniu?Otóż zastanawiam się ile wynosi wynik (-x)^∞ gdzie x należy do liczb dodatnich.
Proszę o Pana uzasadnienie wprowadzenia do tego zestawu symboli nieoznaczonych 0 do potęgi nieskończoność?
To nie jest symbol nieoznaczony, znalazł się tam przez pomyłkę. Przepraszam, poprawiam.
witam!
Czy mógłbym Pan rozpisać rozwiazanie zadania 10 z działu Granic, lekcji 4(twierdzenie o trzech ciągach) ?
Bardzo proszę.
\underset{n\to \infty }{\mathop{lim }}\left[ n\left( \frac{1}{{{n}^{2}}+1}+\frac{1}{{{n}^{2}}+2}+\frac{1}{{{n}^{2}}+3}+\ldots +\frac{1}{{{n}^{2}}+n} \right) \right]
Ograniczam od dołu i od góry:
n\left( \frac{1}{{{n}^{2}}+n}+\frac{1}{{{n}^{2}}+n}+\frac{1}{{{n}^{2}}+n}+\ldots +\frac{1}{{{n}^{2}}+n} \right)\le n\left( \frac{1}{{{n}^{2}}+1}+\frac{1}{{{n}^{2}}+2}+\frac{1}{{{n}^{2}}+3}+\ldots +\frac{1}{{{n}^{2}}+n} \right)\le n\left( \frac{1}{{{n}^{2}}+1}+\frac{1}{{{n}^{2}}+1}+\frac{1}{{{n}^{2}}+1}+\ldots +\frac{1}{{{n}^{2}}+1} \right)
Obliczam granice z ograniczeń z dołu i z góry:
\underset{n\to \infty }{\mathop{lim }}n\left( \frac{1}{{{n}^{2}}+n}+\frac{1}{{{n}^{2}}+n}+\frac{1}{{{n}^{2}}+n}+\ldots +\frac{1}{{{n}^{2}}+n} \right)=\underset{n\to \infty }{\mathop{lim }}n\left( \frac{n\cdot 1}{{{n}^{2}}+n} \right)=\underset{n\to \infty }{\mathop{lim }}\frac{{{n}^{2}}}{{{n}^{2}}+n}=\underset{n\to \infty }{\mathop{lim }}\frac{{{n}^{2}}}{{{n}^{2}}\left( 1+\tfrac{1}{n} \right)}=1
\underset{n\to \infty }{\mathop{lim }}n\left( \frac{1}{{{n}^{2}}+1}+\frac{1}{{{n}^{2}}+1}+\frac{1}{{{n}^{2}}+1}+\ldots +\frac{1}{{{n}^{2}}+1} \right)=\underset{n\to \infty }{\mathop{lim }}n\left( \frac{n\cdot 1}{{{n}^{2}}+1} \right)=\underset{n\to \infty }{\mathop{lim }}\frac{{{n}^{2}}}{{{n}^{2}}+1}=\underset{n\to \infty }{\mathop{lim }}\frac{{{n}^{2}}}{{{n}^{2}}\left( 1+\tfrac{1}{{{n}^{2}}} \right)}=1
Zatem na mocy twierdzenia o trzech ciągach granica tego ciągów równa jest 1.
Jeśli mamy nieskończoność + nieskończoność to jest to symbol oznaczony prawda ?
Tak, ale takiego zwrotu jak: “symbol oznaczony” nie ma.
Prawidłowo powinno się powiedzieć: “to nie jest symbol nieoznaczony”.
Witam.
Mam problem z tym zadaniem:
Pokaż, że 2arctg(x) + arcsin(2x/1+x^2)=π*sgn(x), dla abs(x)>=1.
Proszę o pomoc.
Witam !
Proszę o wyjaśnienie(najlepiej rozpisanie obliczeń) do takiej granicy(z wyjaśnieniem gdy n zmierza do nieskończoności oraz do -nieskończoności):
(-5+4^(-1+n))/(-7+4^n)
Wyniki z wolframalpha
https://www.wolframalpha.com/input/?i=%28-5%2B4%5E%28-1%2Bn%29%29%2F%28-7%2B4%5En%29&lk=1&a=ClashPrefs_*Math-
Przy n dążącym do -nieskończoności? A to jest granica ciągu?
Przy n do +nieskończoności to pójdzie tak (metodami z mojego Kursu):
\underset{n\to \infty }{\mathop{lim }}\frac{-5+{{4}^{-1+n}}}{-7+{{4}^{n}}}=\underset{n\to \infty }{\mathop{lim }}\frac{-5+{{4}^{-1}}{{4}^{n}}}{-7+{{4}^{n}}}=\underset{n\to \infty }{\mathop{lim }}\frac{{{4}^{n}}\left( \tfrac{-5}{{{4}^{n}}}+{{4}^{-1}} \right)}{{{4}^{n}}\left( \tfrac{-7}{{{4}^{n}}}+1 \right)}={{4}^{-1}}=\frac{1}{4}
Zakładając, że to NIE jest granica ciągu, tylko np. funkcji, w której zmienna oznaczona jest jako “n”:
\underset{n\to -\infty }{\mathop{lim }}\frac{-5+{{4}^{-1+n}}}{-7+{{4}^{n}}}=
\left[ \frac{-5+{{4}^{-1-\infty }}}{-7+{{4}^{-\infty }}} \right]=\left[ \frac{-5+{{4}^{-\left( 1+\infty \right)}}}{-7+\tfrac{1}{{{4}^{\infty }}}} \right]=\left[ \frac{-5+\tfrac{1}{{{4}^{1+\infty }}}}{-7+\tfrac{1}{{{4}^{\infty }}}} \right]=\left[ \frac{-5+\tfrac{1}{\infty }}{-7+\tfrac{1}{\infty }} \right]=\left[ \frac{-5+0}{-7+0} \right]=\left[ \frac{5}{7} \right]
\underset{n\to -\infty }{\mathop{lim }}\frac{-5+{{4}^{-1+n}}}{-7+{{4}^{n}}}=\frac{5}{7}
Nie wiem, czy pan jeszcze odpowiada na komentarze, ale mam pewne pytanie.
Jak wiadomo [ \infty – \infty ] to symbol nieoznaczony, który mówi, że od czegoś bardzo dużego odejmujemy coś bardzo dużego.
Co jednak kiedy mamy sytuację [- \infty + \infty ], gdzie do czegoś bardzo małego dodajemy coś bardzo dużego. Czy to jest to samo co poprzednie, czy nie?
To samo 🙂
we wzorach w kursie granice jest taki wzór na “a do potęgi nieskończoność”. I tam jest że gdy a = 1, to “a do potęgi nieskończoność”=1 ale to jest symbol nieoznaczony, więc o co z tym chodzi.
Dzięki, to dobre pytanie.
Chodzi o to, że znak “1” użyty w symbolu nieoznaczonym: \left[ {{1}^{\infty }} \right]i znak “1” użyty we wzorze na {{a}^{\infty }}: {{a}^{\infty }}=\{ \begin{matrix}
\infty \quad dla a>1 \\
1\quad dla a=1 \\
0\quad dla \left| a \right|<1\end{matrix}
…oznaczają coś innego.
W symbolu nieoznaczonym \left[ {{1}^{\infty }} \right]"jedynka" oznacza ("symbolizuje") liczbę nieskończenie blisko liczby 1 (bardziej fachowo powiedziało by się: wyrażenie, którego granicą jest 1).
We wzorze na {{a}^{\infty }}"jedynka" oznacza po prostu liczbę równo 1.
Stąd różnice w "wynikach".
Jeśli liczbę nieskończenie blisko jedynki pomnożymy przez liczbę nieskończenie blisko jedynki pomnożymy przez liczbę nieskończenie blisko jedynki itd. w nieskończoność nie można od razu powiedzieć, jaki będzie wynik takiej operacji (symbol nieoznaczony).
Jeśli jednak równo jeden pomnożymy przez 1 potem pomnożymy przez 1 itd. w nieskończoność wiadomo, że wynikiem będzie 1.
Na tej samej zasadzie symbol "0" w każdym symbolu nieoznaczonym nie oznacza liczby równo 0, a symbol \infty nie oznacza jakiejś konkretnej, bardzo wielkiej liczby.
Więcej na ten temat może Pan przeczytać w tym poście, zapraszam:
https://blog.etrapez.pl/granice/granica-ciagu/klopoty-z-symbolami-nieoznaczonymi/