Analogia z twierdzeniem o trzech ciągach
Odpowiednikiem twierdzenia z granic ciągów, zwanego „twierdzeniem o trzech ciągach” w granicach funkcji jest „twierdzenie o trzech funkcjach”. Leci ono zupełnie analogicznie: jeżeli mamy jakąś funkcję, ograniczoną z góry i z dołu przez jakieś inne funkcje (ograniczoną, tzn. że ich wartości są odpowiednio większe lub mniejsze od wartości tej funkcji) i te funkcje z góry i z dołu zbiegają do tej samej granicy w punkcie lub nieskończoności – to funkcja ta również zbiega do tej granicy w tym punkcie lub nieskończoności.
Zamotane? Dlatego właśnie wynaleziono zapis matematyczny, tam wygląda to prościej, spójrz:
Założenia:
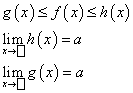W prostokąciku może być liczba, do której dążą x, albo nieskończoność z dowolnym znakiem.
Teza:
Pamiętamy z ciągów? Pamiętamy na pewno…:)
Jak liczy się więc granicę funkcji korzystając z twierdzenia o trzech funkcjach?
Najpierw znajdujesz odpowiednie oszacowanie z góry i z dołu, później liczysz granice z tych oszacowań, pokazując, że są sobie równe i skończone, trzeba już tylko napisać ładną odpowiedź.
Przykład
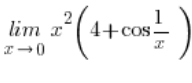
Granice z sinusami i cosinusami szacujemy standardowo jedynką, korzystając z faktu, że cosinus/sinus czegokolwiek jest zawsze mniejszy lub równy od 1 i większy lub równy od -1. Prawdziwa jest więc nierówność:
czyli:
Teraz liczmy granice oszacowań z góry i z dołu (a właściwie nie liczymy, bo są bardzo proste…):
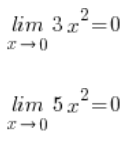
Wyszły takie same (i o to chodzi). Zatem piszemy już tylko odpowiedź:
Odp. Na mocy twierdzenia o trzech funkcjach: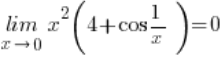 
P.S.
Poniżej, zmieniając „przybliżenie” (otoczenie punktu x_0 = 0 , czyli przy x\to 0 ) możecie sprawdzić, jak funkcje ograniczające x^2 ( 4-1 ) i x^2 ( 4+1 ) ograniczają wykres funkcji z przykładu, czyli x^2 ( 4+\cos\frac{1}{x} ) :
11 Comments
Paula
Witam.Jak będzie wyglądało rozpisanie tego przykładu, arctg nie wiem czy zapisac raz jako -5*pi/4 i raz +5*pi/4?lim ((-1)^(2n+5)*n^2+5*arctg(3+n))/(2*n^2+(-1)^n*n), n->infinity
Lesio
Kiedy twierdzenie o trzech funkcjach, a kiedy twierdzenie o dwóch funkcjach wystarczy do rozwiązania zadania? Jak stosować twierdzenie o dwóch funkcjach? Zgadywać kiedy pasuje tw o dwóch a kiedy o trzech?
Michał
witaj! mam problem z całka a mianowicie Całka xe^-x dx oraz pochodną f(x)=(2x)^(3x) w obu przypadkach jest do potęgi w pierwszym przypadku jest tylko -x w potędze a w drugim 3x jest całe w potędze z góry dziekuje 🙂
Piotr
Witam. A pomógłby mi ktoś z tym przykładem? Lim x-> niesk (x- sin3x)/(2x+sin4x) właśnie z tw. o 3 funkcjach. z Góry dzięki 🙂
Krystian Karczyński
Odpowiedziałem tutaj, zapraszam:
https://blog.etrapez.pl/granice/granice-funkcji/twierdzenie-o-trzech-funkcjach-video/
tyr
Strasznie to głupawo uproszczone i ignoranckie. W twierdzeniu o 3 funkcjach tak się składa że można przyjąć że zachodzi nierówność w dowolnym otoczeniu, w którym to otoczeniu mamy policzyć granicę- i funkcje w tym punkcie są zbieżne do g, wtedy środkowa funkcja jest do tego zbieżna; przy czym nierówność zachodzić może tylko w małym przedziale.
Oczywiście zupełnie nic o tym nie ma, nie ma nawet jasno napisane przy x dążącym do nieskończoności, czy nierówność zachodzić ma od pewnego momentu, czy dla wszystkich x z dziedziny funkcji- krótko mówiąc strasznie głupawo nieskładnie i niedopowiedzianie; pokazane w pseudoprosty sposób pomijając wiele ważnych ścisłych spraw teoretycznych.
Magdalena
Moja kolezanka kupila panski kurs. Razem rozwiazywałysmy zadania. Po drodze natknelam sie na pewne przeszkody. Dlaczego no w takim wyrazeniu : tgx – sinx/ x^3 nie stosujemy twierdzenia na 3 ciągi?
Krystian Karczyński
Witam,
Rozumiem, że chodziło Pani o twierdzenie o trzech funkcjach (a nie ciągach), prawda?
A skąd taki pomysł, żeby akurat w tej granicy zastosować twierdzenie o trzech funkcjach?
Krystian Karczyński
Pytanie dobre, ale odpowiedź niestety z konieczności gorsza.
Nie ma jakiegoś „złotego środka”, reguły, zasady, tabelki z możliwościami. Do każdego przypadku trzeba podchodzić indywidualnie.
Standardowe przypadki to sinus i cosinus, oraz [pmath](-1)^n[/pmath] ,a w pozostałych trzeba po prostu… kombinować. Niestety.
Krystian Karczyński
Dzięki, pewno, że nie jest trudna 🙂
Krzysztof
Dzięki Wielkie Panie Krystianie:)
Wyrazy szacunku dla Pana. (szkoda że nie Pan nie jestem moim sorem od Matematyki, Wtedy matem była by taka prosta i piękna a nie to co teraz:(
Ale dobrze że jest Pan i Pana posty i filmiki:) Bardzo mi pomagają w pojęciu matem. która jak jest dobrze wyłożona wcale nie jest trudna:D:D:D