Kalkulator do granic funkcji dwóch zmiennych
Krystian Karczyński
Założyciel i szef serwisu eTrapez.
Magister matematyki Politechniki Poznańskiej. Korepetytor matematyki z wieloletnim stażem. Twórca pierwszych Kursów eTrapez, które zdobyły ogromną popularność wśród studentów w całej Polsce.
Mieszka w Szczecinie. Lubi spacery po lesie, plażowanie i kajaki.
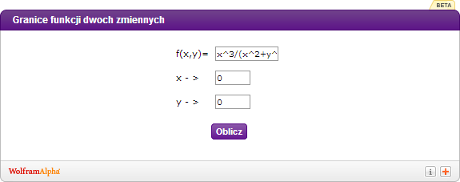
Granice funkcji dwóch zmiennych to troszkę bardziej zaawansowany temat, ale nie na tyle, żeby nie zrobić do niego kalkulatora:
W pole “f(x,y)=” wpisujesz wyrażenie, którego granicę chcesz policzyć, oznaczając zmienne jako “x” i “y” (sprawdź, jak wpisywać wyrażenia matematyczne tutaj).
W pola “x – >” i “y – >” wpisujesz, do czego dążą x i y. Nieskończoność możesz wpisać jako “infinity”, albo “oo” (czyli po prostu dwie małe literki “o”).
Uwaga
Sorry, ale kalkulator nie odróżnia sytuacji, kiedy granica NIE ISTNIEJE, od sytuacji, kiedy granica ISTNIEJE, ale jest niewłaściwa i równa \infty , albo -\infty .
Przykład 1
\underset{\begin{smallmatrix}x\to 0 \\y\to 0\end{smallmatrix}}{\mathop{\lim }}\,\frac{{{e}^{{{x}^{2}}+{{y}^{2}}}}-1}{{{x}^{2}}+{{y}^{2}}}Wpisuję:
“f(x,y) =” (e^(x^2+y^2)-1)/(x^2+y^2)
“x – >” 0
“y – >” 0
Mam wynik:
\underset{\begin{smallmatrix}x\to 0 \\y\to 0\end{smallmatrix}}{\mathop{\lim }}\,\frac{{{e}^{{{x}^{2}}+{{y}^{2}}}}-1}{{{x}^{2}}+{{y}^{2}}}=1Przykład 2
\underset{\begin{smallmatrix}x\to 0 \\y\to 0\end{smallmatrix}}{\mathop{\lim }}\,\left( \sin \frac{1}{{{x}^{2}}+{{y}^{2}}} \right)Wpisuję:
“f(x,y) =” sin(1/(x^2+y^2))
“x – >” 0
“y – >” 0
Mam wynik:
Granica nie istnieje
Przykład 3
\underset{\begin{smallmatrix}x\to 0 \\y\to 0\end{smallmatrix}}{\mathop{\lim }}\,{{\left( 1+{{x}^{2}}+{{y}^{2}} \right)}^{\frac{1}{{{x}^{2}}+{{y}^{2}}}}}Wpisuję:
“f(x,y) =” (1+x^2+y^2)^(1/(x^2+y^2))
“x – >” 0
“y – >” 0
Mam wynik:
\underset{\begin{smallmatrix}x\to 0 \\y\to 0\end{smallmatrix}}{\mathop{\lim }}\,{{\left( 1+{{x}^{2}}+{{y}^{2}} \right)}^{\frac{1}{{{x}^{2}}+{{y}^{2}}}}}=eSzukasz korepetycji z matematyki na poziomie studiów lub szkoły średniej? A może potrzebujesz kursu, który przygotuje Cię do matury?
Jesteśmy ekipą eTrapez. Uczymy matematyki w sposób jasny, prosty i bardzo dokładny - trafimy nawet do najbardziej opornego na wiedzę.
Stworzyliśmy tłumaczone zrozumiałym językiem Kursy video do pobrania na komputer, tablet czy telefon. Włączasz nagranie, oglądasz i słuchasz, jak na korepetycjach. O dowolnej porze dnia i nocy.