Granica ciągu Wykład 4
Temat: Granica niewłaściwa ciągu
Streszczenie
W artykule zdefiniuję, czym są granice niewłaściwe ciągów: ![]() i
i ![]()
![]()
![]()
![]()
![]()
![]()
Granice niewłaściwe ciągów
Jeżeli chodzi o granice ciągów należy odróżniać od siebie trzy sytuacje:
1. Ciągi zbieżne, mające granice.
Może to być na przykład ciąg:
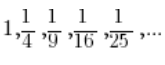
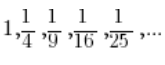
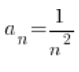
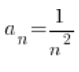
Jest to ciąg, który ma granicę równą 0. Możemy powiedzieć, że “zbiega do zera”.
2. Ciągi rozbieżne, które nie mają granic.
Może to być na przykład ciąg:
![]()
![]()
Ten ciąg nie zbliża się do żadnej liczby. Nie ma granicy w ogóle.
Spośród ciągów rozbieżnych, które nie dążą do żadnej liczby można wyróżnić takie, których kolejne wyrazy są coraz większe (albo odpowiednio: mniejsze) i rozbiegają w nieskończoność (odpowiednio: w minus nieskończoność).
Mogą to być na przykład takie ciągi:
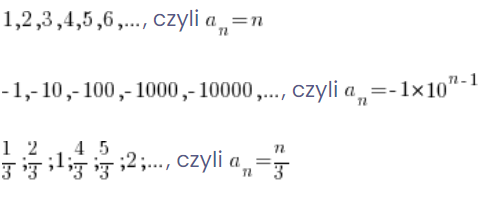
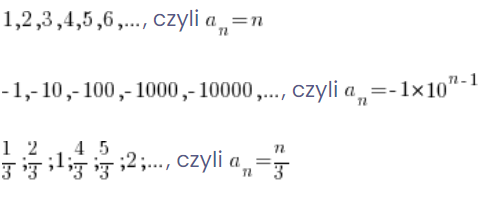
Takie ciągi nazwać możemy:
3. Ciągami rozbieżnymi do ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Jak formalnie zdefiniować tą granicę niewłaściwą? Będzie to swojego rodzaju definicja nieskończoności – rozumianej jako granica niewłaściwa ciągu.
Zastanówmy się… Kiedy powiedzieć można, że ciąg:
![]()
![]()
…rozbiega do ![]()
![]()
![]()
![]()
![]()
![]()
![]()
Powiemy tak: Ciąg ma granicę niewłaściwą ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
A mniej formalnie powiedzieć można, że ciąg ma granicę niewłaściwą ![]()
![]()
![]()
![]()
![]()
![]()
![]()
Co do granic rozbiegających do ![]()
![]()
![]()
![]()
![]()
![]()
Ciąg ma granicę niewłaściwą ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Kliknij, aby przypomnieć sobie, czym są wyrażenia nieoznaczone (poprzedni Wykład) <–

