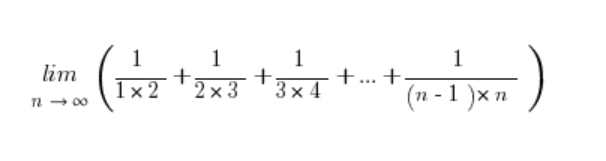
Granica ciągu z sumą nieskończoną
Krystian Karczyński
Założyciel i szef serwisu eTrapez.
Magister matematyki Politechniki Poznańskiej. Korepetytor matematyki z wieloletnim stażem. Twórca pierwszych Kursów eTrapez, które zdobyły ogromną popularność wśród studentów w całej Polsce.
Mieszka w Szczecinie. Lubi spacery po lesie, plażowanie i kajaki.
Weźmy następującą granicę ciągu:
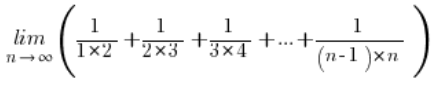
W zadaniu jakoś tak “wyczuwamy”, że trzeba korzystać ze wzorów na sumę ciągu (arytmetycznego lub geometrycznego) ale niestety, niestety… Ten ciąg nie jest ani arytmetyczny, ani geometryczny…
Co robić?
Trzeba to zrobić zupełnie inaczej. Każdy ułamków rozłożyć na ułamki proste. Robi się dosyć intensywnie takie rzeczy przy okazji całek nieoznaczonych wymiernych na przykład. Chodzi o to, żeby znaleźć takie stałe A i B, żeby…
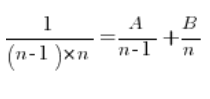
Mnożymy obie strony powyższego równania przez 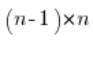 , otrzymując:
, otrzymując:
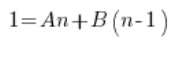
Dalej:
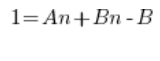
Porównujemy współczynniki wielomianów po lewej i prawej stronie (równość wielomianów – szkoła średnia) i mamy układ równań:
![]() Z drugiego równania:
Z drugiego równania: ![]() .
.
Wstawiając to do pierwszego równania:
![]()
Mamy także ![]() .
.
Nasz dowolny ułamek więc można rozłożyć na:
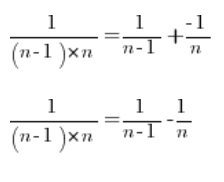
Wracając więc do naszej granicy ciągu i rozkładając każdy z ułamków na ułamki proste:
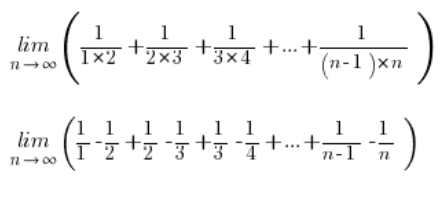
Skracając część składników zostanie nam:
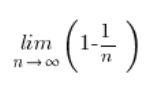
A ta granica ciągu nie jest już straszna, rzecz jasna:
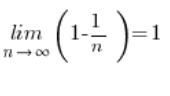
P.S.
Wiele ciekawych przykładów na granice ciągu znajdziesz w moim Kursie Video poświęconym granicom.
Szukasz korepetycji z matematyki na poziomie studiów lub szkoły średniej? A może potrzebujesz kursu, który przygotuje Cię do matury?
Jesteśmy ekipą eTrapez. Uczymy matematyki w sposób jasny, prosty i bardzo dokładny - trafimy nawet do najbardziej opornego na wiedzę.
Stworzyliśmy tłumaczone zrozumiałym językiem Kursy video do pobrania na komputer, tablet czy telefon. Włączasz nagranie, oglądasz i słuchasz, jak na korepetycjach. O dowolnej porze dnia i nocy.










Mam pytanie jak uzasadnić zbieżność ciągu (Xn) i obliczyć jego granicę xn=1/2*3/4*…*2n-1/2n
Czy mógłby Pan wytłumaczyć linijkę skąd się zabrał układ równań A+B=0 oraz -B=1
Tak, jasne. Mamy wielomian:
1=An+Bn-B
Porównujemy za sobą wielomian po lewej i prawej stronie. A konkretnie współczynniki przy odpowiednich potęgach.
Współczynnik przy npo lewej równy jest 0(bo o lewej w ogóle nie ma składnika z n). Współczynnik przy npo prawej jest równy A+B, bo takie są współczynniki przy npo prawej stronie. Stąd równanie:
0=A+B
Wyraz wolny (liczba nie będąca w ogóle współczynnikiem jakiejś potęgi n) po lewej równy jest 1. Po prawej: -B. Stąd równanie:
1=-B
🙂