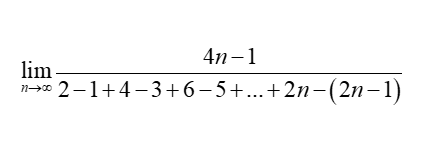
Granica ciągu z dwiema zmiksowanymi sumami ciągów arytmetycznych
Krystian Karczyński
Założyciel i szef serwisu eTrapez.
Magister matematyki Politechniki Poznańskiej. Korepetytor matematyki z wieloletnim stażem. Twórca pierwszych Kursów eTrapez, które zdobyły ogromną popularność wśród studentów w całej Polsce.
Mieszka w Szczecinie. Lubi spacery po lesie, plażowanie i kajaki.
Granice ciągu wykorzystują czasami wzory na sumę ciągów arytmetycznego lub geometrycznego. Gorzej jeśli te ciągi podane są w sposób “zmiksowany” w jednej linijce, tak jak tutaj:
Przykład
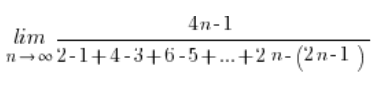
Warto pogrupować inaczej wyrazy w mianowniku, żeby zauważyć, że właściwie są tam dwa ciągi arytmetyczne:
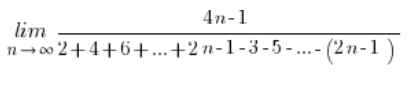
Teraz korzystamy już ze wzorów na sumę:
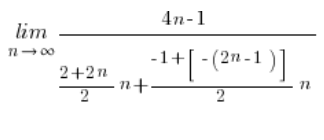
I dalej już tylko liczymy:
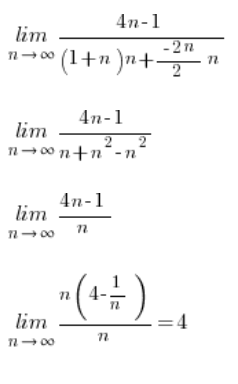
Granica ciągu policzona 🙂
Szukasz korepetycji z matematyki na poziomie studiów lub szkoły średniej? A może potrzebujesz kursu, który przygotuje Cię do matury?
Jesteśmy ekipą eTrapez. Uczymy matematyki w sposób jasny, prosty i bardzo dokładny - trafimy nawet do najbardziej opornego na wiedzę.
Stworzyliśmy tłumaczone zrozumiałym językiem Kursy video do pobrania na komputer, tablet czy telefon. Włączasz nagranie, oglądasz i słuchasz, jak na korepetycjach. O dowolnej porze dnia i nocy.










Tak, ma Pan rację. Poprawiłem to, żeby się nikomu nie myliło.
Dzięki!
Witam zauważyłem w drugiej linijce błąd: po cyfrze 6 nie powinno być -5. Piszę o tym bo chwile myślałem skąd to się zabrało. Pozdrawiam.