Kalkulator do Całek Potrójnych (z konkursem)
Krystian Karczyński
Założyciel i szef serwisu eTrapez.
Magister matematyki Politechniki Poznańskiej. Korepetytor matematyki z wieloletnim stażem. Twórca pierwszych Kursów eTrapez, które zdobyły ogromną popularność wśród studentów w całej Polsce.
Mieszka w Szczecinie. Lubi spacery po lesie, plażowanie i kajaki.
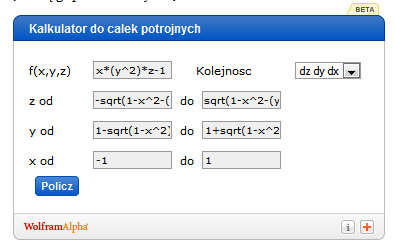
Jakiś już czas temu niezastąpiony Wolfram udostępnił nam swój kalkulator do całek potrójnych (trochę go przetłumaczyłem):
Jak widać powyżej kalkulator jest bardzo prosty.W pierwszej linijce wpisujemy funkcję podcałkową i kolejność całkowania. Klikamy ‘Policz’. Mamy wynik 🙂
Oznaczenia funkcji w Wolframie
Trochę problemów mogą sprawić oznaczenia, np. 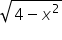 w granicach całkowania Wolframa trzeba by wpisać jako ‘sqrt(4-x^2)’ – jak w przykładzie powyżej. Zajrzyjcie do Ogólnej Instrukcji Wpisywania Formuł Matematycznych i w razie problemów pytajcie śmiało w komentarzach.
w granicach całkowania Wolframa trzeba by wpisać jako ‘sqrt(4-x^2)’ – jak w przykładzie powyżej. Zajrzyjcie do Ogólnej Instrukcji Wpisywania Formuł Matematycznych i w razie problemów pytajcie śmiało w komentarzach.
Kalkulator doskonale radzi sobie z obliczeniami bez współrzędnych walcowych, sferycznych, liczbami  ,
,  – no jednym słowem MIODZIO.
– no jednym słowem MIODZIO.
Przykład 1
Używając kalkulatorka obliczymy sobie całkę potrójną z funkcji 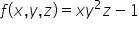 w kuli o równaniu
w kuli o równaniu 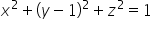
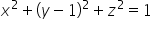
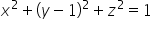
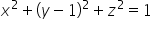
Po narysowaniu obszar całkowania wyglądał by tak (nie pomoże nam w tym na razie kalkulator niestety):
Mając pod ręką kalkulator nie wchodzimy nawet we współrzędne sferyczne, takie z nas leniuchy. Opisujemy obszar całkowania normalnie współrzędnymi x,y,z.
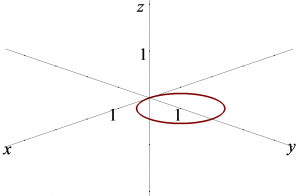
Rzutem kuli na płaszczyznę (powiedzmy) xOy będzie koło:
W tym kółku ‘x’-sy – powiedzmy znowu – niech zmieniają się w stałych granicach od -1 do 1.
‘y’-ki niech zmieniają się w granicach zmiennych, wyliczamy je z równania kuli biorąc za 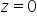
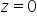
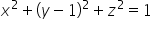
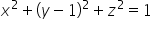
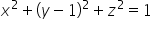
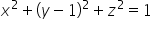
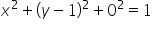
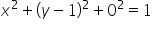
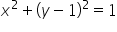
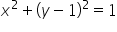
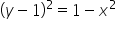
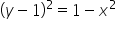
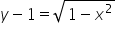
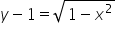
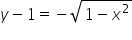
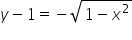
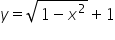
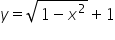
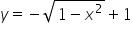
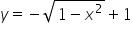
No i mamy dokładnie granice całkowania dla ‘y’. Granice całkowania dla z wyliczamy (będą to powierzchnie) podobnie z równania:
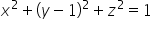
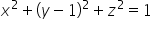
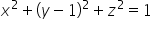
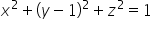
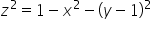
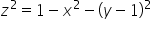
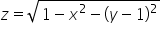
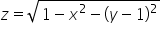
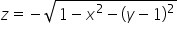
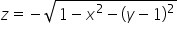
Sprzątaniem zupełnie się nie przejmujemy, bo mamy kalkulator.
Podsumowując:
Mamy funkcję podcałkową: 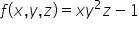
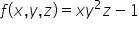
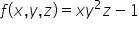
Mamy obszar całkowania:
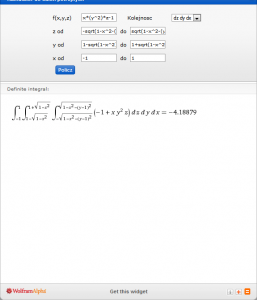
Wpisanie danych do kalkulatora
Funkcję podcałkową i granice całkowania wpisujemy w kalkulator tak:
Kolejność całkowania nam się zgadza (najpierw po ‘z’, potem po ‘y’, na końcu w stałych po ‘x’) czyli już tylko klikamy na ‘Policz’ i mamy wynik:
Mamy więc wynik: -4,18879 , policzony zgrabnie i bez współrzędnych sferycznych.
Szukasz korepetycji z matematyki na poziomie studiów lub szkoły średniej? A może potrzebujesz kursu, który przygotuje Cię do matury?
Jesteśmy ekipą eTrapez. Uczymy matematyki w sposób jasny, prosty i bardzo dokładny - trafimy nawet do najbardziej opornego na wiedzę.
Stworzyliśmy tłumaczone zrozumiałym językiem Kursy video do pobrania na komputer, tablet czy telefon. Włączasz nagranie, oglądasz i słuchasz, jak na korepetycjach. O dowolnej porze dnia i nocy.


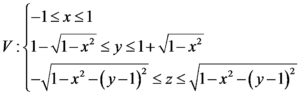







Jak wpisać całkę potrójną w kalkulator?
Nie rozumiem, więc poproszę o przykład.
Dodałem mój przykład do posta. Może jeśli masz jakieś swoje to zapodaj – pokażę, jak je wpisać w kalkulator.
Czy przed końcem maja ukaże się jeszcze kurs o całkach wielokrotnych?
Tak, dam radę go skończyć do końca maja.
Jej dziękuje!:D
A jaki Kurs Pani zamawia?
dziękuje 😉
ja bym chętnie pozyskał kurs całki oznaczonej 😉
PS: Dzięki poprzednim kursom zaliczyłem wszystkie kolokwia i egzamin 😉 Przede mną kolejny i czuje się na siłach aby zaliczyć na solidną ocenę.
Także jest za co dziękować.
Pozdrawiam serdecznie
Ogłaszam zakończenie konkursu. Wygrał p. Sebastian i p. Monika, która też podała w sumie dobrą odpowiedź, tylko nie napisała o jaką konkretnie kulę chodzi.
objętość kuli o promieniu 2
objętość obszaru kuli o promieniu 2
Można po prostu: objętość kuli o promieniu 2. Gratuluję 🙂
objętość obszaru V tej kuli 😉
połowa kuli? ćwierć kuli?
Nie. Nie.
wnętrza kuli,
Jakiego konkretnie wnętrza?
Objętość kuli!;p
A konkretniej czego? 🙂
Czy to nie przypadkiem pole kuli?:)
Nie 🙂
Wynik jest objętością. (V)
O.K. A konkretnie czego objętością?