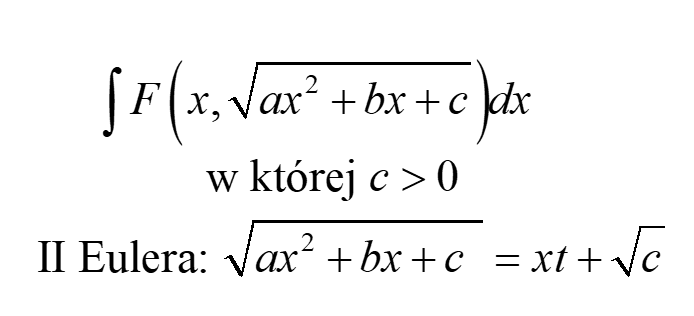
Podstawienia Eulera II rodzaju

---

Podstawienia Eulera I rodzaju (dla a>0) – powtórzenie

W poprzednim poście:

Podstawienia Eulera I rodzaju

zajęliśmy się całkami typu:

,

w których a>0.

Rozbroiliśmy także przykładową całkę spełniającą ten warunek, tzn.

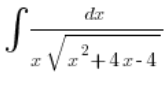
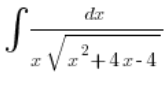
Co jednak, jeśli  w trójmianie będzie ujemne (przypadek, gdy a=0 można pominąć, bo wtedy nie będzie to w ogóle trójmian kwadratowy i całkę rozwiąże się przez podstawienie prostsze , niż podstawienie Eulera) ?

Wtedy pomóc nam może (ale nie musi…) drugi rodzaj podstawień Eulera:

Podstawienie Eulera II rodzaju (dla c>0)

Mając całkę typu:

,

w której c>0, stosujemy podstawienie typu:

,

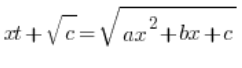
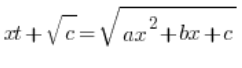
które znowu podnosimy obustronnie do kwadratu, w którym tym razem składniki z się skracają i które trzeba jeszcze podzielić obustronnie przez , żeby wyjść na zależność liniową, z której wyznaczymy przy pomocy zmiennej w kolejności:

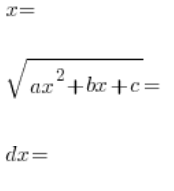
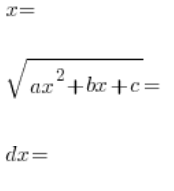
Podstawimy to wszystko do całki:

i wyjdziemy znów na całkę wymierną, która – powtarzam – na ogół jest żmudna.

Ruszajmy więc z przykładem.

Przykład

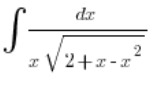
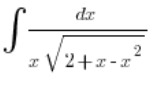
W trójmianie kwadratowym trochę pozmieniana kolejność składników, ale chyba jasne jest, że . Czyli, że  nie jest większe od (nie zastosujemy więc I rodzaju podstawień Eulera), ale c>0 (czyli zastosujemy II rodzaj).

Podstawiamy więc:

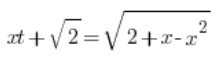
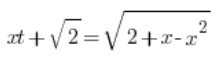
Podnosimy obie strony do kwadratu:

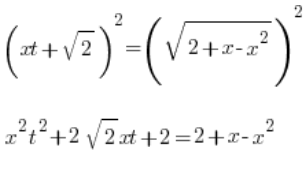
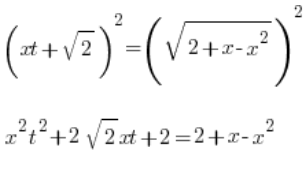
Składnik 2 się skraca (tak ma być):

i teraz coś, czego nie było w I rodzaju podstawień, dzielimy obustronnie przez x:

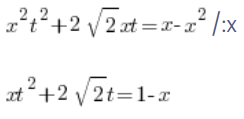
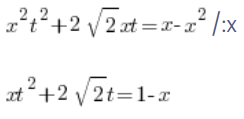
Dalej wyznaczamy x:

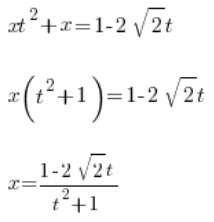
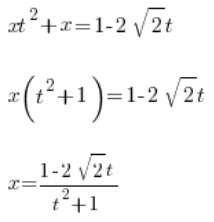
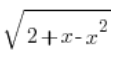
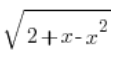
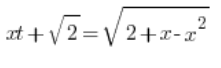
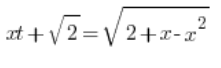
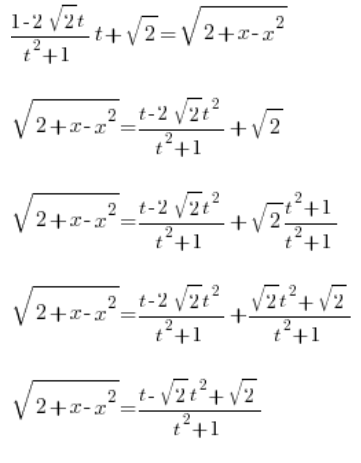
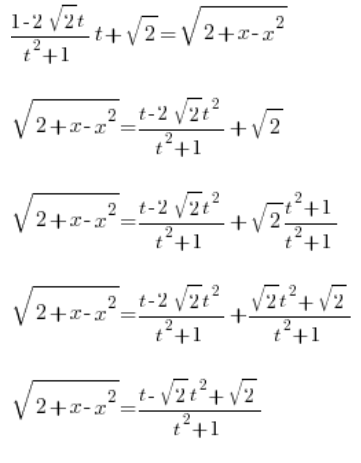
Mamy x wyznaczone przy pomocy zmiennej t. Teraz wyznaczamy . Na początku mieliśmy podstawienie:

 mamy już wyznaczone, więc tylko wstawiamy:

Pozostało nam do wyznaczenia tylko . Obliczymy je licząc pochodną z :

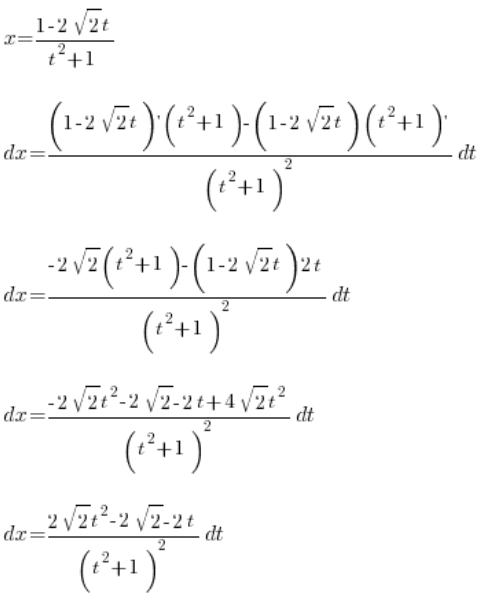
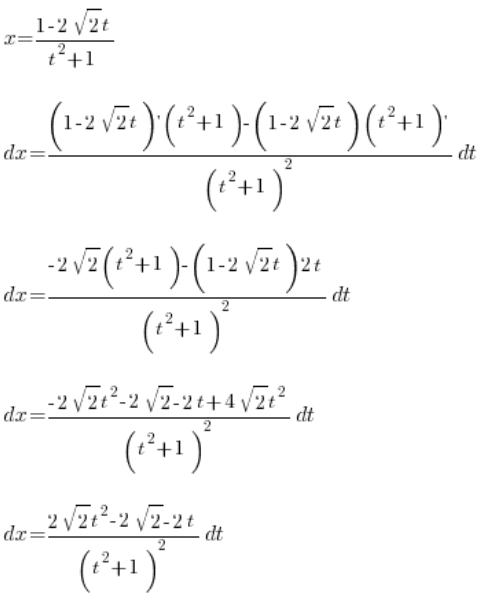
Mamy więc wyznaczone:

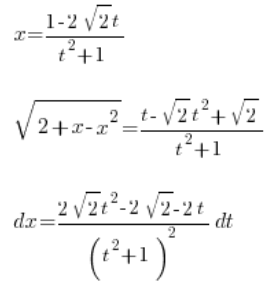
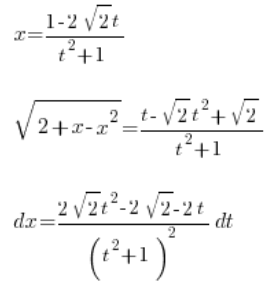
, wszystko przy pomocy zmiennej . Bierzemy całkę:

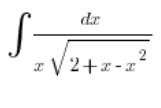
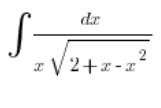
i wstawiamy:

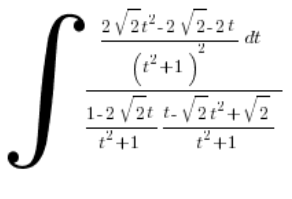
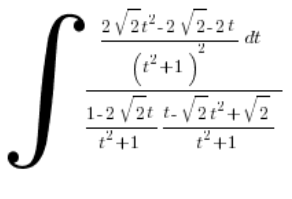
Bierzemy się za sprzątanie:

\int{\frac{-2\left( -\sqrt{2}{{t}^{2}}+\sqrt{2}+t \right)}{\left( 1-2\sqrt{2}t \right)\left( -\sqrt{2}{{t}^{2}}+\sqrt{2}+t \right)}dt} \int{\frac{-2}{1-2\sqrt{2}t}dt}=\left| \begin{matrix}&u=1-2\sqrt{2}t\\&du=-2\sqrt{2}dt\\&dt=\frac{du}{-2\sqrt{2}}\\\end{matrix} \right|=\int{\frac{-2}{u}\frac{du}{-2\sqrt{2}}}=\frac{1}{\sqrt{2}}\int{\frac{du}{u}}=\frac{1}{\sqrt{2}}\ln \left| u \right|+C

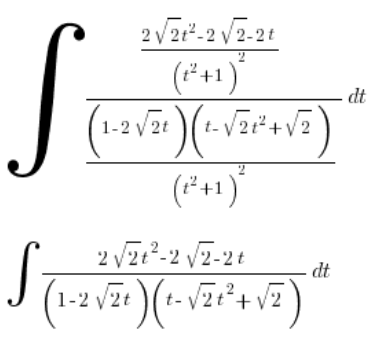
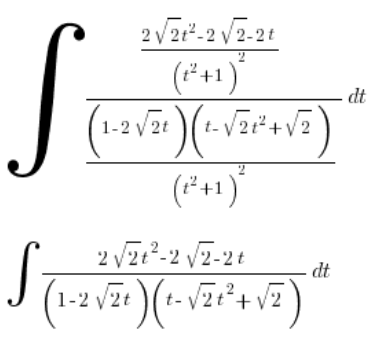
A wracając  się z podstawieniem:

\frac{1}{\sqrt{2}}\ln \left| u \right|+C=\frac{1}{\sqrt{2}}\ln \left| 1-2\sqrt{2}t \right|+C

Trzeba jeszcze wrócić z tdo x. Naszym podstawieniem Eulera było

xt+\sqrt{2}=\sqrt{2+x-{{x}^{2}}}

Skąd

t=\frac{\sqrt{2+x-{{x}^{2}}}-\sqrt{2}}{x}

Czyli nasze rozwiązanie to

\frac{1}{\sqrt{2}}\ln \left| u \right|+C=\frac{1}{\sqrt{2}}\ln \left| 1-2\sqrt{2}t \right|+C=\frac{1}{\sqrt{2}}\ln \left| 1-2\sqrt{2}\frac{\sqrt{2+x-{{x}^{2}}}-\sqrt{2}}{x} \right|+C

Co z innymi przypadkami?

Wiemy, że kiedy w całce:

• a>0 – stosujemy I rodzaj podstawień
• c>0 – stosujemy II rodzaj podstawień

Co jednak, jeśli ani , ani nie są większe od zera? O tym w następnym poście, w którym omówię III rodzaj podstawień Eulera i pokażę, że temat będzie w już wyczerpany, tzn. do każdej całki typu:

…dobierzemy któryś z trzech rodzajów podstawień.