Twierdzenie Fermata. Warunek konieczny istnienia ekstremum.

Ekstrema Funkcji Wykład 6

Temat: Twierdzenie Fermata. Warunek konieczny istnienia ekstremum funkcji.

Streszczenie

Do badania zachowania się funkcji często wykorzystuje się jej pochodną . Na wykładzie przedstawię i udowodnię twierdzenie Fermata, które określa konieczny warunek istnienia ekstremum funkcji w punkcie odwołując się do jej pochodnej. Pokażę także, że nie jest to warunek wystarczający – na przykładzie punktów z funkcji, w których jest on spełniony, a jednak ekstremów w nich nie ma…

Innymi słowy: jeżeli funkcja ma ekstremum w punkcie i ma pochodną w tym punkcie to na pewno, na pewno, na pewno pochodna z funkcji w tym punkcie równa jest zero.

Zwróćmy od razu uwagę (wrócimy do sprawy później), że twierdzenie Fermata nie zachodzi jakby „w drugą stronę”, to znaczy, z tego, że pochodna z funkcji w punkcie równa jest zero nie wynika, że w tym punkcie funkcja osiąga ekstremum.

Czyli jeszcze raz (upraszczając): jeśli mamy ekstremum, to mamy pochodną równą zero.

Aby dowieść Twierdzenie Fermata wprowadzę i udowodnię wcześniej lemat (o monotoniczności funkcji w zależności od jej pochodnej), który przydaje się nie tylko do tego dowodu:

Lemat ogólnie wyraża znaną i stosowaną zależność między zachowaniem się funkcji i jej pochodnej w punkcie.

Na przykład weźmy funkcję i jej pochodną . Narysujmy ich wykresy jeden pod drugim:

Widać, że funkcja jest rosnąca/malejąca w tych samych przedziałach, co jej pochodna przyjmuje wartości większe/mniejsze od zera.

Lemat jest także doskonale „wyczuwalny” intuicyjne: skoro pochodna w punkcie wyraża przyrost wartości dla nieskończenie małego przyrostu argumentów, to jeśli wartość pochodnej będzie dodatnia, to przyrost tych wartości musi być też dodatni (funkcja musi „wzrosnąć”) i na odwrót – funkcja jest rosnąca.

Jeśli pochodna będzie ujemna, wartości musiały „zmaleć” – funkcja będzie malejąca.

Zabierzemy się teraz za ścisły dowód lematu. Aby to zrobić, musimy przypomnieć sobie (ze szkoły średniej) z definicji, co to znaczy, że funkcja „jest rosnąca” w punkcie i co to znaczy, że funkcja „jest malejąca” w punkcie.

Przyjrzyjmy się, jak „działa” te definicja funkcji rosnącej w punkcie na wykresie:

Na wykresie widać, że funkcja jest rosnąca w punkcie . Jest rosnąca, ponieważ istnieje otoczenie prawostronne punktu (na wykresie zaznaczono na czerwono na osi OX) i dla x-sów z tego otoczenia odpowiadające im wartości (zaznaczone na czerwono na osi OY) są większe od wartości funkcji w punkcie (czyli f\left( {{x}_{0}} \right)>f\left( x \right)), a także ponieważ istnieje otoczenie lewostronne punktu (na wykresie zaznaczono na niebiesko na osi OX) i dla x-sów z tego otoczenia odpowiadające im wartości (zaznaczone na niebiesko na osi OY) są mniejsze od wartości funkcji w punkcie (czyli ).

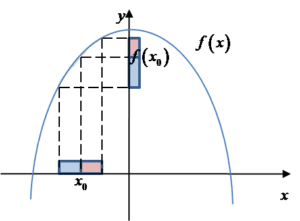
Wiedząc już, co to konkretnie znaczy „rosnąca w punkcie” i „malejąca w punkcie” możemy się zabierać za dowód lematu:

Mając udowodniony lemat o monotoniczności funkcji dowód Twierdzenia Fermata staje się dziecinnie prosty:

Twierdzenie Fermata jako warunek konieczny, ale nie wystarczający istnienia ekstremum funkcji w punkcie

Należy jeszcze raz podkreślić, że warunek konieczny istnienia ekstremum działa tak:

JEŻELI: Funkcja ma ekstremum w punkcie i pochodną w punkcie

WTEDY: Pochodna funkcji w punkcie   równa jest 0

Nie działa on jednak tak:

JEŻELI: Pochodna funkcji w punkcie równa jest 0

WTEDY: Funkcja ma ekstremum w punkcie

To ważne. W praktyce oznacza to, że aby pokazać, że funkcja osiąga ekstremum w punkcie nie wystarczy sprawdzić, czy jej pochodna w tym punkcie równa jest zero.

Przykład

Weźmy funkcję . Jej pochodna równa jest . Jej pochodna w punkcie jest jak najbardziej równa 0 (bo ), ale ekstremum, jak widzimy na wykresie tej funkcji ni ma…

Możliwe są różne inne akcje, na przykład funkcja w punkcie w ogóle nie posiada pochodnej (pokazywałem na Wykładach z pochodnych) – a ekstremum ma jak najbardziej (można narysować i zobaczyć).

Widzimy więc, że samo Twierdzenie Fermata nie wystarczy nam do tego, aby ekstrema funkcji wyznaczać…

KONIEC

Pisząc tego posta korzystałem z…

1. „Rachunek różniczkowy i całkowy. Tom I.” G.M. Fichtenholz. Wyd. 1966.

Kliknij tutaj, aby przypomnieć sobie, czym są ekstrema funkcji (poprzedni Wykład) <–

Kliknij tutaj, aby zobaczyć, jakie warunki są wystarczające do istnienia ekstremum funkcji w punkcie (następny Wykład) –>

Kliknij, aby powrócić na stronę z wykładami o badaniu przebiegu zmienności funkcji